Из вершины В параллелограмма ABCD проведем высоту ВН к стороне AD. Рассмотрим треугольник АВН: угол АНВ = 90 градусов (так как ВН - высота, перпендикуляр), АВ = 6 см (по условию) - гипотенуза (так как лежит против угла 90 градусов), угол ВАН = угол А = 30 градусов (по условию). Катет ВН лежит против угла равного 30 градусов, поэтому:
ВН = АВ/2 (свойство прямоугольного треугольника);
ВН = 6/2 = 3 (см).
Площадь параллелограмма находится по формуле:
S = a*h,
где а - сторона параллелограмма, h - высота, опущенная на сторону а.
S = AD*BH;
S = 10*3 = 30 (см квадратных).
ответ: S = 30 см квадратных.
№1.
Как проверить: подставляем координаты в уравнение. Если все совпадает - пара является решением уравнения, если нет - то нет.
(3;1)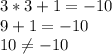 
(0;10)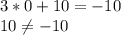 
(2;4)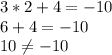 
(3;2,5)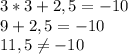 
ответ: если дано уравнение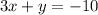 
, то ни одна пара не является решением уравнения; если дано уравнение 
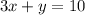, то подходят пары (3;1), (0;10) (2;4).
Примечание: просто я не понял, отрицательное или положительное ли число 10 во второй части данного уравнения, поэтому расписал на оба случая.
№2.
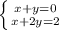
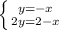
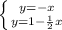
(смотри рисунок)
ответ: (-2;2)
№3.
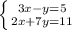
Метод подстановки:
Выражаем у в первом уравнении:
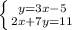
Подставляем значение у во второе уравнение:
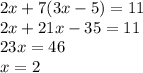
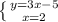
Подставляем значение х в выраженный у, чтобы найти его:
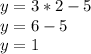
Метод сложения:
Сначала умножим левую и правую части первого уравнения на 7, чтобы можно было сократить у в каждом из уравнений.
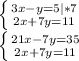
Теперь почленно складываем первое и второе уравнения в одно целое:
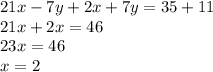
Подставляем найденный х в любое из уравнений. Я возьму первое уравнение.
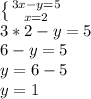
ответ: (2;1)
180 м/мин=3м/с
3+29=32 м/с