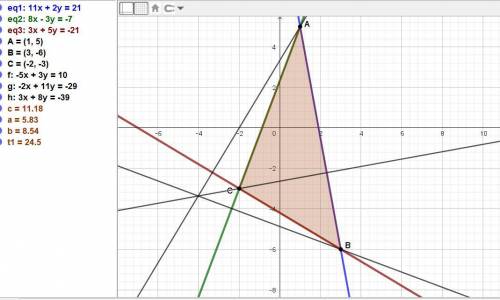
Даны уравнениям сторон треугольника:
11x+2y-21=0
8x-3y+7=0
3x+5y+21=0.
В уравнении перпендикулярной прямой коэффициенты А и В в уравнении вида Ах + Ву + С = 0 меняются на -В и А.
Возьмём первую сторону (пусть это АВ, получаем уравнение высоты из точки С: -2х + 11у + С = 0. Чтобы определить слагаемое С уравнения надо подставить координаты точки, через которую проходит прямая.
Находим вершины треугольника, решая системы из двух уравнений сторон. Точка А:
{11x+2y-21=0 |x(3) = 33x + 6y - 63 = 0
{8x-3y+7=0 |x(2) = 16x - 6y + 14 = 0
49x - 49 = 0, х = 49/49 = 1.
у = (21 - 11х)/2 = (21 - 11*1)/2 = 10/2 = 5. Точка А(1; 5).
Аналогично определяем точки: В(3; -6) и С(-2; -3).
Теперь находим С в уравнении высоты из точки С.
-2*(-2) + 11*(-3) + С = 0,
С = 33 - 4 = 29. Уравнение -2х + 11у + 29 = 0.
Аналогично находим уравнения высот из точек А и В.
Высота из точки А: -5х + 3у - 10 = 0,
из точки В: 3х + 8у + 39 = 0.
Пошаговое объяснение:
Ход решения задачи.
1.
Провести через вершину меншего основания прямую, паралельную боковой стороне трапеции.
Получим на основании 2 отрезка, один из которых равен 2, другой - 1см( равный меньшему основанию)
2.
Обозначить отрезок между основанием высоты и большим углом у основания х
Составить 2 выражения для нахождения высоты трапеции (из того же угла), для чего опустить эту высоту на большее основание и приравнять их.
Получим
h²=()²-х²
h²=4² - (2-х)²
(2√3)²-х²=4² - (2-х)²
Решив это уравнение. найдем, что х=0.
Отсюда эта трапеция - прямоугольная, и углы при меньшей боковой стороне - прямые.
h=2√3
Косинус нужного угла =2:4=0,5
Найдите угол по таблице косинусов.
Этот угол равен 60º.
типотиплрл
Пошаговое объяснение:
ипомарт рнщ