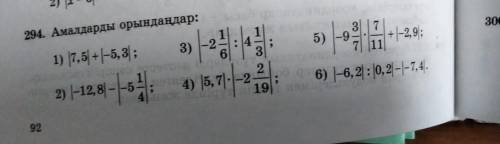
шестиугольников было всего 2.
Пошаговое объяснение:
Каждый пятиугольник дает 5 вершин, шестиугольник - 6. Пусть пятиугольников было х, шестиугольников у. Тогда получаем уравнение с двумя неизвестными:
5х +6у = 32.
Поскольку вершин 32, то не могло быть так, что все фигуры были пятиугольниками (иначе бы число вершин оканчивалось 0 или 5). Максимум шестиугольников могло быть 32:6 = 5 ост 2. Остаток в 2 вершины нас не устроит, так как из них "не собрать" пятиугольник. Остаток должен быть кратен 5 (5, 10, 15 и так далее). Нечетные остатки получить не получится (6у заведомо четное число, а при вычитании из 32 ответ получится четным). Значит лишних вершин могло быть 10 или 20. Если их было 10, то на шестиугольники остается 22 вершины, что не кратно 6. Значит на пятиугольники пришлось 20 вершин, а на шестиугольники - 12. Отсюда - шестиугольников было всего 2.
Рассмотрим простой пример:
15:5=3
В этом примере натуральное число 15 мы поделили нацело на 3, без остатка.
Иногда натуральное число полностью поделить нельзя нацело. Например, рассмотрим задачу:
В шкафу лежало 16 игрушек. В группе было пятеро детей. Каждый ребенок взял одинаковое количество игрушек. Сколько игрушек у каждого ребенка?
Поделим число 16 на 5 столбиком получим:
Деление с остатком
Мы знаем, что 16 на 5 не делиться. Ближайшее меньшее число, которое делиться на 5 это 15 и 1 в остатке. Число 15 мы можем расписать как 5⋅3. В итоге (16 – делимое, 5 – делитель, 3 – неполное частное, 1 — остаток). Получили формулу деления с остатком, по которой можно сделать проверку решения.
16=5⋅3+1
a=b⋅c+d
a – делимое,
b – делитель,
c – неполное частное,
d – остаток.
Не знаю, какой это язык, но решить примеры могу:
| | просто делает числа положительными, так что это просто примеры, в которых ничего сложного нет
1) 12,8 2) 7,55 3) 0,5 4) 12 5) 8,9 6) 23,6