ответ дан
1. Вычислите: −2 • (54 − 129)=-2*(-75)=150.
2. Вычислите: −3 • (72 − 138)=3*(-66)=198.
3. Вычислите: 4 • (43 − 150)=4*(-107)=-428.
4. Вычислите: 6 • (25 − 131)=6*(-106)=-636.
5. Вычислите: (31 − 12) • (32 − 62)=19*(-30)=-570.
6. Вычислите: (13 − 44) • (27 − 47)=-31*(-20)=620.
7. Вычислите: (39 − 57) : (27 − 18)=-18:9=-2.
8. Вычислите: (63 − 84) : (14 − 21)=-21:(-7)=3.
9. Вычислите: −2 • (11 − 36)=-2*(-25)=50.
10. Вычислите: 5 • (74 − 93)=5*(-19)=-95.
11. Вычислите: (7 − 13) • (192 − 184)=-6*8=-48.
12. Вычислите: (87 – 68 – 22) : 3=-3:3=-1.
13. Вычислите: (63 − 75) • (110 − 115)=-12*(-5)=60.
14. Вычислите: (12 + 63 – 36) : (− 13)=39:(-13)=-3.
15. Вычислите: 32 – 41 + 54 – 73=-28.
Позже дополню
Вероятность выбросить комбинацию {5; 6} складывается из двух возможностей:
- на первом кубике выпало 5, а на втором выпало 6;
- на первом кубике выпало 6, а на втором выпало 5.
Вероятность выпадения каждого числа равна в отдельности:
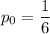
Тогда, вероятность выбросить комбинацию {5; 6} при броске двух кубиков складывается из двух несовместных событий (перечислены выше), каждое из которых представляет собой комбинацию независимых событий (выпадение первого и второго кубика):
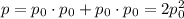

Соответственно, вероятность не выбросить эту комбинацию соответствует вероятности противоположного события:
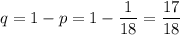
Вероятность не выбросить нужную комбинацию при двух бросках дважды определяется по правилу умножения вероятностей независимых событий:
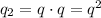
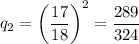
Эта вероятность соответствует ситуации, когда гости не получат комплимент. Значит, противоположное событие - гости получат комплимент, оно произойдет с вероятностью:

ответ: 0.11