Автобус - х км/ч
Грузовая машина - х + 18 км/ч
S - 420 км
t встречи - 3 ч
Найти:
Скорость автобуса и скорость грузовой машины - ? км
Пусть х км/ч - скорость автобуса, тогда х + 18 км/ч - скорость грузовой машины. По условию задачи они выехали одновременно и встретились через 3 часа, расстояние между городами - 420 км. Составим и решим уравнение:
3х + 3(х+18) = 420
3х + 3х + 54 = 420
6х = 420 - 54
6х = 366
х = 366 : 6
х = 61
1) 61 (км/ч) - скорость автобуса
2) 61 + 18 = 79 (км/ч) - скорость грузовой машины
ответ: скорость автобуса — 61 км/ч;
скорость грузовой машины — 79 км/ч.
1)Симметрия — слово греческого происхождения, как и многие другие слова, которые связаны с математикой. Оно означает соразмерность, наличие определённого порядка, закономерности в расположении частей.
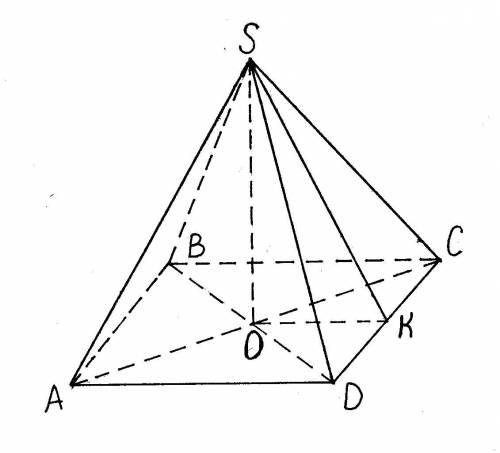
2)Квадрат. Правильная четырёхугольная пирамида - это многогранник, у которого одна грань является основанием квадратом, а другие грани, боковые, являются равнобедренными треугольниками с общей вершиной.
3) самое 1 фото ниже
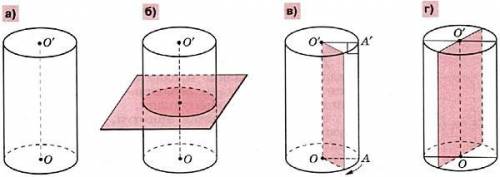
4)Цилиндр — геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её.
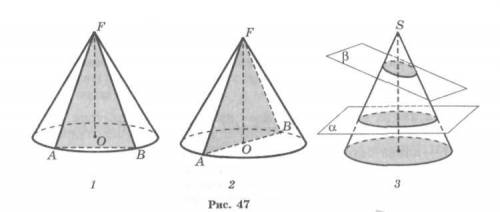
Конус — тело, полученное объединением всех лучей, исходящих из одной точки (вершины конуса) и проходящих через плоскую поверхность.
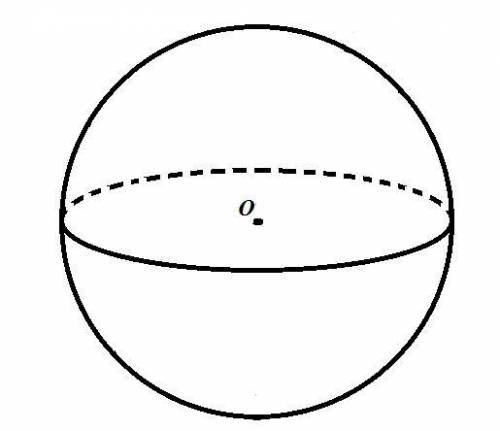
Шар — геометрическое тело; совокупность всех точек пространства, находящихся от центра на расстоянии, не больше заданного.
5) цилиндр-фото где 4 примера с красными линиями(а,б,в,г)
конус-с серыми линиями
шар-просто обычный круг
Теперь, когда эта пара нашлась, существует всего только 364 дня в году, не совпадающих с днем рождения "счастливчиков".
В худшем случае,
не родиться в один день со счастливчиками и
не превзойти лишь пару рожденных в один день
могут только 364+364 = 728 человек.
ясно, что кроме этих двоих "счастливчиков" у нас как раз и осталось уже не 730, а ровно 730-2 = 728 человек с неизвестными нам днями рождения.
Значит существует только один расклад, при котором нет тройки рожденных в один день. (При этом в этом раскладе абсолютно все дни "использованы" в кач-ве дней рождения дважды.)
сколько же раскладов дают тройку именинников в один день?
Логика подсказывает, что 728 раз по 1/365...
Я бы так подвел итог своих соображений: только один расклад Не дает нам наличия в институте третьего студента, рожденного в один день со "счастливчиками" и 728 дают наличие такого студента с вероятностью 1/365 каждый
Пойдет такое решение?
дело в том, что я не могу сообразить, как в числах посчитать вероятность получившуюся: ясно, что раз есть хоть один расклад без тройки именинников, то общая вероятность меньше 1 (т.е. меньше 100%), но как посчитать конкретный процент - не соображу что-то...