Дано уравнение √(2x+4) = 1 - 2x.
ОДЗ: 2x + 4 ≥ 0, х ≥ -2,
1 - 2x ≥ 0, х ≤ 1/2.
Вывод: обе части его - положительны.
Левая часть - возрастающая функция, правая - убывающая.
Значит, есть одна точка пересечения, в которой справедливо равенство (если оно существует).
Возведём его в квадрат: 2x + 4 = 1 - 4x + 4x².
4x² - 6x - 3 = 0. Д = 36 + 4*4*3 = 84. √84 = 2√21.
х1 = (6 + 2√21)/8 = (3 + √21)/4 ≈ 1,89564. По ОДЗ не принимаем.
х2 = (6 - 2√21)/8 = (3 - √21)/4 ≈ -0,39564.
ответ: корень один и равен х = (3 - √21)/4 ≈ -0,39564.
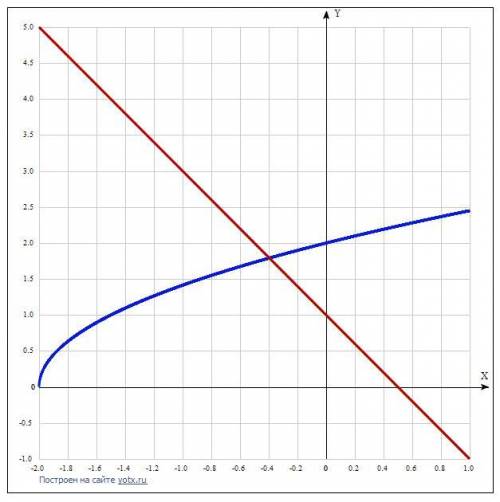
ответ можно подтвердить графически: ведь корень - это точка пересечения двух графиков у = √(2x+4) и у = 1 - 2x.
ответ: Пятерок больше на 4.
Пошаговое объяснение:
Пусть а-восьмиклассников с 1 пятеркой, б(2)-восьмиклассников с двумя пятерками, в-число восьмиклассников с тремя пятерками и 2в-число восьмиклассников с нулевым кол-вом пятерок.
Тогда всего восьмиклассников: а+б+3в
А их количество пятерок:
а+2б+3в+0×2в=а+2б+3в.
Видно, что кол-во пятерок > восьмиклассников на 2б=2*2(по условию)