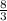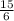.
. Готово.
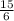и , где числитель дроби — общее число бросков, а ее знаменатель — число попаданий. Видно, что при одинаковом числе попаданий, второй баскетболист совершил меньше бросков, а значит и его результат лучше.
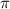в математике, по определению, равно отношению длинны 
произвольной окружности к диаметру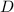 
той же окружности, поскольку все окружности подобны друг другу, т.е.:
;
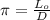формула [1] ;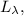
составляющую 
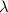часть от длины всей окружности, в данном конкретном случае 
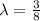от длины всей окружности, то нам просто нужно умножить длину всей окружности на эту самую часть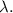 
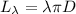формула [2] ;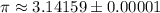
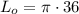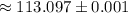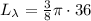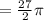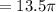см 
см ;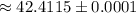
см 
см 
см 
см ;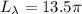
см ;
см .
ответ:это дроби вот 4\4 8\8 2 6\7
Пошаговое объяснение:
это тип сказана так