35 = 5 · 7; 42 = 2 · 3 · 7; НОД = 7
35/42 = 5/6 - сократили на 7
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
13 - простое число; 78 = 2 · 3 · 13; НОД = 13
13/78 = 1/6 - сократили на 13
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
7 - простое число; 14 = 2 · 7; НОД = 7
7/14 = 1/2 - сократили на 7
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
75 = 3 · 5²; 100 = 2² · 5²; НОД = 5² = 25
75/100 = 3/4 - сократили на 25
Радиус основания = R*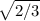
, высота = R * 2/
.
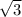Пошаговое объяснение:
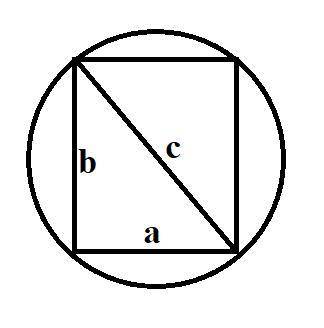
Посмотрим на шар сбоку (см. рис). Тогда цилиндр мы будем видеть как прямоугольник. Пусть, a - диаметр круга в основании цилиндра, b - высота цилиндра. Тогда объем цилиндра вычисляется по формуле
V = pi * (a/2)² * b = (pi/4) * a²b
Чтобы объем был максимальным, нужно, чтобы величина a²b была максимальной. Заметим, что a² = c²-b² = 4R² - b²
max(a²b) = max((4R²-b²)*b)
Пусть, f(b) = (k-b²)*b, где k = 4R².
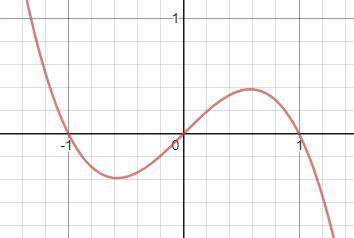
Эта функция имеет график, как на рисунке, т.е. проходит через точку (0;0). Нас интересует максимум при b>0. Он достигается в точке, где f'(b) = 0.
f'(b) = k - 3b² = 0.
b = +-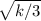 
b = -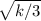 не подходит, т.к. b положительно.
Значит, b = 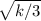= R * 2/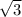
a =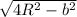 
= 
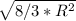= R * 2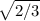, радиус основания в 2 раза меньше, т.е. R*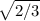
43200-8s=5536
-8s=5536-43200
-8s=-37664
s=4708
2) t:(6400-6393)=8500
t:7=8500
t=8500*7
t=59500