1) -3 + (-7) = -3 -7 = -10
2) -3 -7 = -10
3) -3 + 7 = 7 - 3 = 4
4) -3 - (-7) = (так как - на - даёт + то) = -3 + 7 = 7 - 3 = 4
5) -(-3) -(-7) = 3 + 7 = 10 (опять же - на - даёт плюс)
6) -(-3) + 7 = 3 + 7 = 10
7) -(-3) + (-7) = 3 - 7 = -4
8) -(-3) - 7 = 3 - 7 = - 4
9) 3 - 7 = -4
10) 3 + 7 = 10
11) 3 - (-7) = 3 + 7 = 10
12) 3 + (-7) = 3 - 7 = -4
a) -27 + 49 = 22
б) -27 + (-49) = -76 (по принципу: -1 -3 = -4)
в) -27 -49 = -76
г) 27 - 49 = -22
д) 27 + (-49) = 27 - 49 = -22
е) -(-27) -(-49) = 27 + 49 = 76
ж) -(-27) -49 = 27 - 49 = -22
з) -(-27) + 49 = 27 + 49 = 76
и) -(-27) + (-49)
к) -6 + (-0,6) = -6 - 0,6 = -6,6
л) 3,6 + (-2,4) = 3,6 - 2,4 = 1,2
м) -1,26 + 1,26 = 0
И в следующие разы загружай фотку нормально!
ответ: Изначально стаканов машинного масла у Бипа было 26 , у Бопа 14 , у Бупа 8
Пошаговое объяснение:
Пусть
У Бипа x ст
У Бопа y ст
У Бупа z ст
После того как каждый дал другу кол-во стаканов с маслом , сколько было у этого друга .
То у каждого их них в конце стало по 16 стаканов с маслом
У Бипа 16 ст
У Бопа 16 ст
У Бупа 16 ст
Теперь важно понять , что общее кол-во стаканов в начале у каждого равно общему кол-ву стаканов в конце .
(То есть кол-во стаканов в начале никак не изменилось в конце )
В конце у них было 16+16+16 = 48 стаканов
Значит изначально у них было 48 стаканов
То есть x+y+z = 48
1 Шаг
Сначала Бип раздал каждому другу столько же стаканов с маслом , сколько было было у этого друга
То есть
У Бипа стало x-y-zс т
У Бопа стало 2y ст
У Бупа стало 2z ст
2 ШагЗатем Боп сделал тоже самое
Тогда
У Бипа стало 2(x-y-z) ст
У Бопа стало (2y-2z -x+y+z) =3y-z-x ст
У Бупа стало 4z ст
3 Шаг
И наконец Буп раздал каждому другу столько же стаканов с маслом , сколько было было у этого друга , и у каждого из них стало по 16 ст с маслом
Тогда
1) У Бипа стало 4(x-y-z) = 16 ст
2) У Бопа стало 2(3y-z-x) = 16 ст
3) У Бупа стало 4z - (3y - z - x) -2(x-y-z) = 7z - y - x = 16 ст
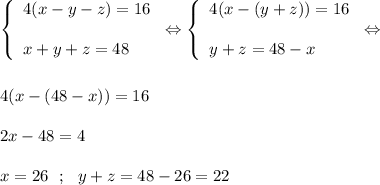
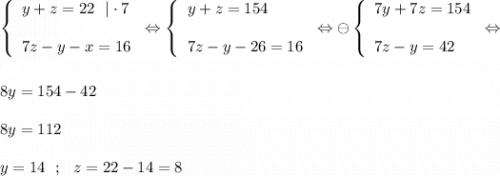
4) Также мы знаем что x+y+z = 48
Составим систему из 1 и 4 уравнения
Из уравнений
y+z =22
7z - y - x = 16
Составим еще одну систему (учитывая что x = 26 )