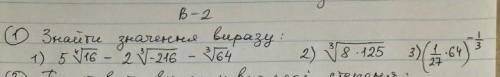
Представим города, как вершины графа, а дороги, как рёбра.
Изначально у нас был полный граф на 30 вершин, следовательно, в нём было (30 * 29 : 2 = 435) рёбер. Минимальный связный граф - дерево. В дереве на 30-ти вершинах будет 29 рёбер, следовательно, убрать можно не более (435 - 29 = 406) рёбер. Пример - уберём все рёбра из полного графа на 29 вершин, тогда уберётся (29 * 28 : 2 = 406) рёбер, а из любой вершины можно будет добраться до другой через 30-ую вершину, которую мы не трогали.
ответ: 406 дорог.
Х - первый ящик;
У - второй ящик;
К- третий ящик;
Е - четвертый ящик.
Тогда из условия:
Х + У + К =12 кг. лука (не менее);
Х + У + Е =9 кг. лука (не более);
У+ К + Е =7 кг. лука (не более);
Х + К + Е =8кг. лука (не более)
Слаживаем левые и правые части уравнение:
Х +У + К + Х + У + Е + У + К + Е + Х + К + Е=12+9+7+8
3Х+3У+3К+3Е=36
3(Х+У+К+Е)=36
Х+У+К+Е=36/3=12 кг.лука было в четырех ящиках.
Х + У + К =12 кг. лука , а в Х + У + К + Е =12 кг. Следовательно в ящике Е (четвертый) лука не было.
Х + У + Е =9 кг. лука, а в Х + У + К + Е =12 кг. Следовательно в ящике К (третий) лука было 12-9=3 кг.
У+ К + Е =7 кг. лука, а в Х + У + К + Е =12 кг. Следовательно в ящике Х (первый) лука было 12-7=5 кг.
Х + К + Е =8кг. лука, а в Х + У + К + Е =12 кг. Следовательно в ящике У (второй) лука было 12-8=4 кг.
Проверка:
Х + У + К = 5+4+3=12 кг. лука - верно
Х + У + Е =5+4+0=9 кг. лука - верно
У+ К + Е =4+3+0=7 кг. лука - верно
Х + К + Е =5+3+0=8кг. лука - верно
ответ: в первом ящике было 5 кг.
во втором ящике было 4 кг
в третьем ящике было 3 кг.
в четвертом ящике лука не было.