
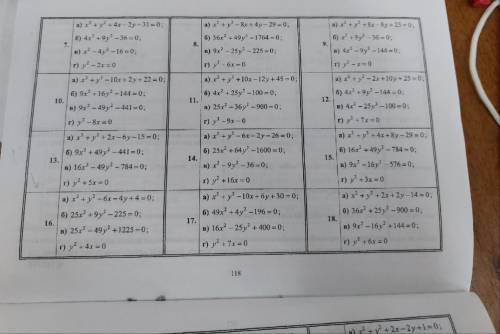
Задание 1.
\tt\displaystyle x=\frac{400+8,5*(-46)}{24,5-(-70)*(-0,25)}=\frac{400-391}{24,5-17,5}=\frac{9}{7}x=
24,5−(−70)∗(−0,25)
400+8,5∗(−46)
=
24,5−17,5
400−391
=
7
9
35% = 35% : 100% = 0,35
\tt\displaystyle 0,35*\frac{9}{7}=\frac{35}{100}*\frac{9}{7}=\frac{35:5}{100:5}*\frac{9}{7}=\frac{7}{20}*\frac{9}{7} =\frac{9}{20}=0,450,35∗
7
9
=
100
35
∗
7
9
=
100:5
35:5
∗
7
9
=
20
7
∗
7
9
=
20
9
=0,45
Задание 2
{47,3:(-11)-4,7}{-23,23:(-0,23)-110} =\frac{-4,3-4,7}{101-110}=\frac{-9}{-9}=1x=
−23,23:(−0,23)−110
47,3:(−11)−4,7
=
101−110
−4,3−4,7
=
−9
−9
=1
12% = 12% : 100% = 0,12
\tt\displaystyle 0,12*1=0,120,12∗1=0,12
у=2х+1
у=2х-3
у=х+7
Эти линейные функции вида у=kx+b, где k-это угловой коэффициент, с его изменением будет меняться угол наклона прямой к оси Ох, значит, функции с одинаковыми угловыми коэффициентами будут параллельны друг другу. Отсюда параллельные функции:
у=2х+1 и у=2х-3. Эти графики функций можно построить по двум точкам каждый. Находим точки:
у=2х+1
х=0
у=2*0+1=0+1=1
(0;1)
х=1
у=2*1+1=3
(1;3)
у=2х-3
х=0
у=2*0-3
у=-3
(0;-3)
х=1
у=2*1-3=-1
(1;-1)
у=х+7
х=0
у=7
(0;7)
х=2
у=2+7=9
(2;9)
По этим точкам строим графики.
2)
Поскольку графики прямые, два из которых параллельны, то эти 2 графика будут пересекать третий, т.е. у=2х+1 и у=2х-3 будут пересекать график у=х+3, а график у=х+7 пересекать его не будет, т.к. он с тем же угловым коэффициентом.
Для нахождения координат пересечения приравняем функции:
2х+1=х+3
2х-х=3-1
х=2
у=2+3=5
координата пересечения (2;5)
2х-3=х+3
2х-х=3+3
х=6
у=6+3=9
(6;9)
Графики в файле...