ответ: 15 см.
Дано: Параллелепипед - аквариум.
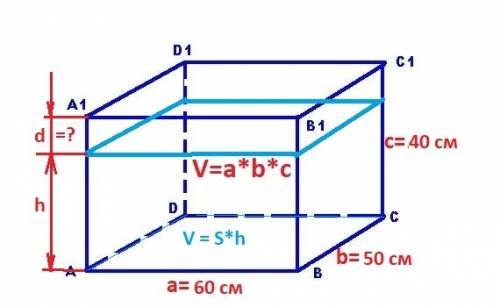
a = 60 см длина
b = 50 см ширина
c = 40 см - высота
v = 75 л - объём воды.
Найти: d = ? - расстояние до верха аквариума.
Пошаговое объяснение:
Рисунок к задаче в приложении.
1 л = 1000 см³ - единицы объёма.
Объём аквариума по формуле:
V = a*b*c = 60*50*40 = 120 000 см³ = 120 л - аквариум.
Можно составить пропорцию для высоты воды.
40 см : 120 л = h : 75 л
h = 40 * 75/120 = 25 см - высота воды.
d = c - h = 40 - 25 = 15 см - до края аквариума - ответ.
Или по другой формуле:
v = 75 л = 75 000 см³ - объём воды.
v = S*h = a*b*h = 60*50*h = 300*h = 75 000 см³
h = 75000 : 300 = 25 см - уровень воды.
d = c - h = 40 - 25 = 15 см - ответ.
Подробнее - на - ответ:
Пошаговое объяснение:
ответ: 15 см.
Дано: Параллелепипед - аквариум.
a = 60 см длина
b = 50 см ширина
c = 40 см - высота
v = 75 л - объём воды.
Найти: d = ? - расстояние до верха аквариума.
Пошаговое объяснение:
Рисунок к задаче в приложении.
1 л = 1000 см³ - единицы объёма.
Объём аквариума по формуле:
V = a*b*c = 60*50*40 = 120 000 см³ = 120 л - аквариум.
Можно составить пропорцию для высоты воды.
40 см : 120 л = h : 75 л
h = 40 * 75/120 = 25 см - высота воды.
d = c - h = 40 - 25 = 15 см - до края аквариума - ответ.
Или по другой формуле:
v = 75 л = 75 000 см³ - объём воды.
v = S*h = a*b*h = 60*50*h = 300*h = 75 000
h = 75000 : 300 = 25 см - уровень воды.
d = c - h = 40 - 25 = 15 см - ответ.
Подробнее - на -
Пошаговое объяснение:
Из условия известно, что стороны параллелограмма равны 8 см и 10 см. Так же известно, что меньшая высота равна 4 см. Найти же нам нужно длину второй высоты.
Применим для этого мы формулу для нахождения площади параллелограмма:
S = a * ha.
Площадь параллелограмма равна произведению стороны на высоту, опущенную на эту сторону.
Для a = 10 см и высоты ha = 4 см ищем площадь параллелограмма.
S = 10 * 4 = 40 см^2.
Для второй стороны запишем формулу:
S = b * hb.
hb = S/b;
Подставляем значения и производим вычисления:
hb = 40/8 = 5 см вторая высота.
ответ: 5см