Викреслити графік функції μ=(0,01λ)3+Noз.п. в інтервалі зміни значень аргументу від 300 до 1000 з кроком - id2051510920210503 от fara32 03.05.2021 07:27

Question

Математика: Викреслити графік функції μ=(0,01λ)3+Noз.п. в інтервалі зміни значень аргументу від 300 до 1000 з кроком 100. Заштрихувати площу, обмежену функціональною кривою та горизонтальною лінією, що проходить через точку з координатою μ=500+Noз.п. Зростання значення аргументу відповідає напрямку вісі ОХ, функції - вісі ОУ.

fara32 · Accepted Answer

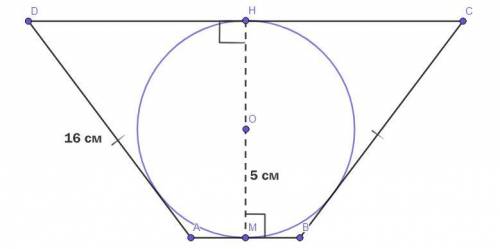
Дано :

Четырёхугольник ABCD - равнобедренная трапеция (AB║DC, AD = BC).

Окружность с центром О - вписанная в равнобедренную трапецию окружность.

ОМ - радиус окружности = 5 см.

AD = BC = 16 см.

Найти :

S(ABCD) = ?

Если в четырёхугольник можно вписать окружность, то суммы противоположных сторон равны.

Следовательно -

AD + BC = AB + DC.

Но так как -

AD = BC = 16 см.

Поэтому -

AD + BC = 16 см + 16 см = 32 см

AB + DC = 32 см.

Радиус вписанной в трапецию окружности равен половине высоты.

На чертёже НМ - высота ABCD, следовательно -

НМ = 2*ОМ

НМ = 2*5 см

НМ = 10 см.

Площадь трапеции равна произведению полусуммы оснований и высоты.

То есть -

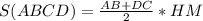
$S(ABCD) =\frac{AB+DC}{2} *HM$

Теперь в формулу подставляем известные нам численные значения и считаем -

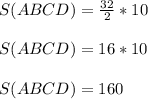
$S(ABCD) =\frac{32 }{2} *10\\\\S(ABCD)=16*10\\\\S(ABCD)=160$

ответ : 160 (ед²).

Вравнобедренную трапецию с боковой стороной, равной 16см, вписана окружность с радиусом, 5см. найдит

MOGZ ответил