Первого футболиста можно выбрать второго третьего Таким образом получаем 11 * 10 * 9=990 вариантов выбора. Однако, каждая тройка нападающих, при этом подсчете, учтена несколько раз: одна и та же тройка нападающих может быть выбрана по разному, например, сначала "1", потом "2", потом "3", или сначала "3", потом "1", потом "2" и т.д. Поскольку число перестановок из трех элементов равно 3!, то каждая тройка нападающих учтена нами 3! = 6 раз. Поэтому 990 : 6 = 165 вариантов троек нападающих.
Mov esi, massiv mov ecx, size lodsd ; читаем первый mov ebx, eax ; делаем его максимальным m1: test ecx, ecx ; конец массива? jz m2 dec ecx ; уменьшаем счетчик lodsd ; читаем след элемент массива cmp eax, ebx ; если меньше максимального jl m1 ; читаем дальше mov ebx, eax ; иначе его делаем максимальным jmp m1 ; и читаем дальше m2: ; конец массива ... massiv dd ??, massiv - указатель на начало массива size - размер массива (константа) , либо [size] если переменная lodsd грузит из [esi] один dword в eax и смещает esi на следующий элемент для байтовых массивов lodsb, для 2байтовых lodsw eax - текущий элемент ebx - максимальный
-3cos(x)+x∧4-x+C
Пошаговое объяснение:
-3cos(x)+4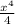 -x+C
-x+C