(1) a^20
(2) b^30
(3) c^4
(4) d^30 (
5) c^5 (6)
k^84
(^ - знак степени)
Пошаговое объяснение:
Правило один: Если степень возводится в другую степень, то они перемножаются.
Пример: (a^2)^2 = a^4
Правило два: Если число в одной степени умножается на другое число в другой степени, то числа перемножаются , а степени складываются.
Пример: a^4 × a^4 = a^8
Правило три: Если число в одной степени делится на другое число в другой степени, то числа делятся, а степени вычитаются.
Пример: a^7 : a^4 = a^3
(2^2 : 1^2 = 4 : 1 = 4)
а) к≠3, любое из чисел. например -9, или 14 - единственное решение.
не имеет решений, когда к=3 прямые параллельны, общих точек нет.
чтобы система имела решение, надо, чтобы прямые совпадали. т.е. к=3, а вместо 4 поставить -5, но т.к. уже 4 подобрана, то подобрать невозможно.
б) аналогично. упростим первое у=1.5х,
единсвт. решение , когда угловые коэф. различные -подобрать невозможно. при к-2 бесконечное множество решений. прямые совпадут. а при к≠-2 решений нет. т.к. прямые параллельны.
в)у=0.5-кх/2; у=0.5-4х
При к=8 бесконечное число решений, при к≠8 единственное, а для того, чтобы система не имела решений, к подобрать невозможно, т.к. уже совпадают 0.5 и 0.5- это ординаты точек пересечения графиков с осью оу.
Відповідь:
Покрокове пояснення:
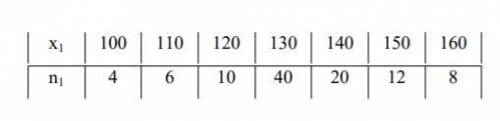
Число наблюдений =100
а) моду;
М =130, так как чаще всего встречается, 40 раз
б) медиану;
100/2=50
50 член вариационного рада - 130
51 член - 130
Поэтому медиана = 130
в) выборочную среднее;
Х=1/100×(100×4+110×6+120×10+130×40+140×20+150×12+160×8)=13340/100=133,4
г) выборочную дисперсию;
Х²=1/100×(100²×4+110²×6+120²×10+130²×40+140²×20+150²×12+1602×8)=1 799 400/100=17994
D=17994-133,4²=198,44
д) выборочное среднее квадратическое отклонение;
D^½=14,087
е) коэффициент вариации.
14, 087÷133,4=0,106