Если стороны пропорциональны числам 4;9 и 6 ,значит одна сторона состоит из 4 частей,вторая из 9 частей и третья из 6 частей,причем одна часть одинаковая для всех.
например.а) самая короткая сторона длиной 18см состоит из 4 частей,
18:4=4,5 см это 1 часть
4,5*9=40,5 см это сторона,состоящая из 9 частей
4,5*6=27 см это сторона,состоящая из 6 частей
б) средняя сторона длиной 18см состоит из 6 частей,
18:6=3 см это 1 часть
3*4=12см это сторона,состоящая из 4 частей
3*9=27 см это сторона,состоящая из 9 частей
с) самая длинная сторона длиной 18см состоит из 9 частей,
18:9=2 см это 1 часть
2*4=8см это сторона,состоящая из 4 частей
2*6=12см это сторона,состоящая из 6 частей
 . Есть константа(число) и переменные, содержащие степень. А например
. Есть константа(число) и переменные, содержащие степень. А например 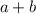 одночленом уже не будет.
одночленом уже не будет.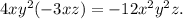 .
. 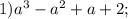
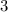

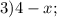
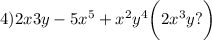
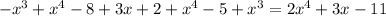
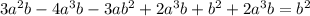
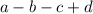 в виде:
в виде: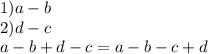
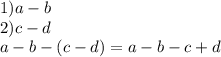
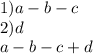

 и
и 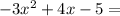 .
.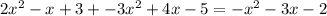
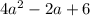 и
и 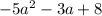 .
.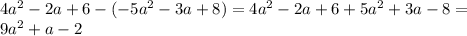
 и
и 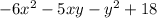 .
.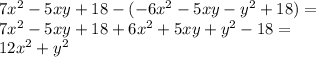
1) В - 3√3 см
2) Б - 6 см
3) Г - 3√5 см
Пошаговое объяснение:
Маємо правильну чотирикутну піраміду SABCD, в основі якої лежить правильний чотирикутник (квадрат) ABCD.
Висота SO правильної трикутної піраміди проектується у центр квадрата ABCD – точку перетину діагоналей AC і BD. Оскільки висота SO перпендикулярна до площини основи (квадрата ADCD), то вона перпендикулярна до кожної прямої, що лежить в цій площині.
Проведемо відрізок ОК⊥ДС . Оскільки SO⊥ОК, ОК⊥ДС, то за теоремою «про три перпендикуляри» SК⊥ДС. (SК - апофема Т.як ΔSCD - рівнобедрений, то SК- медіана (ДК=КС) ).
Звідси слідує, що ∠SКO=60° – лінійний кут двогранного кута при основі – кут нахилу бічної грані до площини основи. ∠SOК=90°)
1) Висота піраміди
ΔSКO (∠О=90°): ∠ОSК = 30°,Катет прямокутного трикутника, що лежить проти кута в 30 °, дорівнює половині гіпотенузи ⇒ ОК=1/2*SK = 3см.
За теоремою Піфагора: SО²= SК²-ОК²
SО=√(36-9)=√27=3√3см
2) Ребро основи піраміди
Так як ABCD - правильний чотирикутник (квадрат), то АД=2*ОК=2*3=6см
3) Бічне ребро піраміди
ΔSКС(∠К=90°): За теоремою Піфагора SС² = SК²+ КС²
SС = √(36+9)=√45=3√5см