ответ:
х₁ = х₂ = -12, х₃ = х₄ = -0,8
пошаговое объяснение:
существует четыре варианта:
1) при котором подмодульное значение первого модуля отрицательное, а второго положительное:
|3x + 8| = |4 - 2x|
-3x - 8 = 4 - 2x
-3x + 2x = 4 + 8
-x = 12
x₁ = -12
2) при котором подмодульное значение первого модуля положительное, а второго отрицательное:
|3x + 8| = |4 - 2x|
3x + 8 = 2х - 4
3x - 2x = -4 - 8
x = -12
x₂ = -12
3) при котором оба подмодульных выражения положительные:
|3x + 8| = |4 - 2x|
3x + 8 = 4 - 2x
3x + 2x = 4 - 8
5x = -4
x₃ = -0,8
4) при котором оба подмодульных выражения отрицательные:
|3x + 8| = |4 - 2x|
-3x - 8 = 2х - 4
-3x - 2x = -4 + 8
-5x = 4
x₄ = -0,8
Пусть первая прямая имеет угловой коэффициент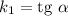 
, а вторая прямая имеет угловой коэффициент 
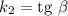, где 
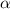и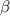 
- соответствующие углы наклона прямых к положительному направлению оси 
.
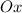Рассмотрим угол между этими прямыми. Пусть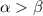 
, тогда он равен 
. Найдем соотношение между этим углом и угловыми коэффициентами прямых. Используем формулу тангенса разности:
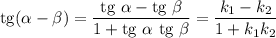
Так как мы хотим получить условие перпендикулярности двух прямых, то считаем угол между прямыми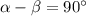 
.
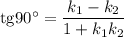
Тангенс 90 градусов не определен, но можно сказать что он стремится к бесконечности к стремлении аргумента к 90 градусам.
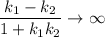
Но если дробь стремится к бесконечности, то знаменатель стремится к нулю.
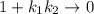
В пределе знаменатель равен нулю. Тогда получим:
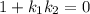
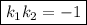
Можно выразить один из коэффициентов:
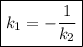
Тогда формулируется легкое правило: Две прямые перпендикулярны, когда их угловые коэффициенты являются противоположными обратными числами.
На картинке. Желаю удачи.