Представим 30 в виде произведения:
30 = 2*3*5
Произведение пяти последовательно взятых чисел будет делиться на 30, если в этом произведении найдутся числа, которые будут делиться на 2, на 3 и на 5.
На два делятся все четные числа. Четным числом является каждое второе число. Поскольку мы берем пять последовательных чисел, то четные числа точно будут. Значит произведение будет делиться на 2.
На три делится каждое третье число. Мы же берем пять последовательно стоящих чисел. Поэтому число, которое делится на 3 тоже найдется.
На пять делится каждое пятое число. Опять же, мы берем пять последовательно стоящих чисел, поэтому в произведении найдется число, которое будет делиться на пять.
В результате среди пяти последовательно стоящих чисел обязательно найдутся числа, которые будут делиться на 5, на 3 и на 2. Поэтому произведение пяти последовательно стоящих чисел будет делиться на 30.
Например, возьмем следующие пять последовательных чисел: 94, 95, 96, 97, 98.
94 - четное число и поделится на 2.
96 нацело поделится на 3.
95 поделится на 5.
Следовательно произведение 94*95*96*97*98 нацело поделится на 30.
ДАНО: y(x) = x⁴ - 2x³+3
ИССЛЕДОВАНИЕ.
1. Область определения D(y) ∈ R, Х∈(-∞;+∞) - непрерывная , гладкая.
2. Вертикальная асимптота - нет - нет разрывов.
3. Наклонная асимптота - y = k*x+b.
k = lim(+∞) Y(x)/x = +∞ - нет наклонной (горизонтальной) асимптоты.
4. Периода - нет - не тригонометрическая функция.
5. Пересечение с осью OХ.
Нули функции:нет.
6. Интервалы знакопостоянства.
Положительная -Y(x)>0 X∈(-∞;+∞) - во всём интервале определения.
7. Пересечение с осью OY. Y(0) = 3.
8. Исследование на чётность.
В полиноме есть и чётные и нечётные степени - функция общего вида.
Y(-x) ≠ Y(x) - не чётная. Y(-x) ≠ -Y(x) - ни нечётная.
9. Первая производная. Y'(x) = 4*x³ - 6*x² = 4*x²*(x- 1.5) = 0
Корни Y'(x)=0. Х₁ = 0, X₂= 0, Х₃= 1.5
Производная отрицательна между корнями - функция убывает.
10. Локальные экстремумы.
Минимум - Ymin(0) = 3. Максимум - Ymax(0) = 3. Минимум - Ymin(X₃ = 1,5) = 1,3125.
11. Интервалы монотонности.
Убывает - Х∈(-∞;0]∪[0;1.5], возрастает - Х∈[1.5;+∞).
12. Вторая производная - Y"(x) = 12*x² -12*x = 12*x*(x - 1) = 0
Корень производной - точки перегиба - Х=0, Х = 1.
13. Поведение.
Вогнутая – «ложка» Х∈(-∞; 0]∪[1;+∞).
Выпуклая “горка» Х∈[0; 1]
14. График в приложении.
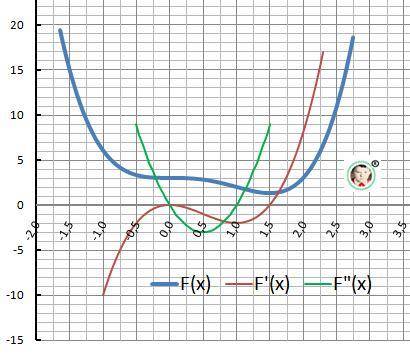
ответ в файле выше ^