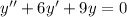
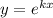 .
.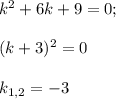
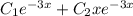
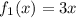 и
и 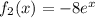
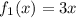
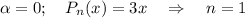
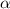 с корнями характеристического уравнения, и, принимая во внимания, что n=1, частное решение будем искать в виде.
с корнями характеристического уравнения, и, принимая во внимания, что n=1, частное решение будем искать в виде.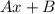
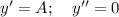 , подставим в исходное уравнение без функции
, подставим в исходное уравнение без функции 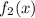 .
.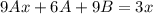
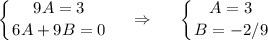
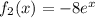
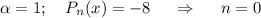
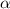 с корнями характеристического уравнения и принимая во внимая, что n=0, частное решение будем искать в следующем виде:
с корнями характеристического уравнения и принимая во внимая, что n=0, частное решение будем искать в следующем виде: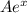
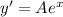 и
и 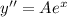
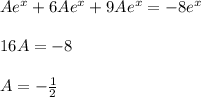
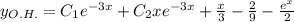
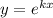 .
.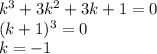
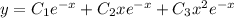
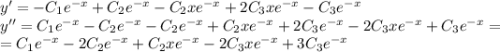
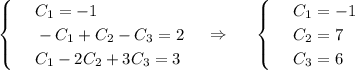
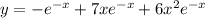
а) 3+2= 5 долей
48: 5= 9,6 л
9,6 *3 = 28,8 л
9,6 *2 = 19,2
3:2 = 28,8:19,2
б) 7+3 =10
48:10 = 4,8
7* 4,8 = 33,6
3 * 4,8 = 14,4
7:3 = 33,6 : 14,4
Сплав состоит из олова и свинца, массы которых
относятся как 2 : 4. Масса сплава 13,7 кг. Сколько в этом сплаве олова и
сколько свинца?
2+4 = 6 частей
13,7 : 6 *2 = 4,6 кг - олова
13,7 : 6* 4 = 9,1 кго - свинца