
24·x²–34·x+25·y²=39
Пошаговое объяснение:
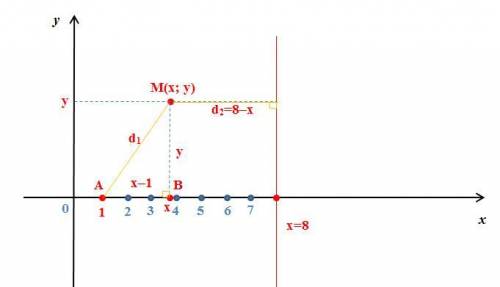
Пусть (x; y) координаты точки M, то есть M(x; y), d₁ – расстояние от точки M(x; y) до точки А(1; 0), а d₂ – расстояние от точки M(x; y) до прямой x=8.
Проекцией точки M(x; y) на ось Ох будет точкой В(x; 0) (см. рис). Тогда расстояние d₁ можем найти из прямоугольника треугольника AMB с катетами
АВ = (х–1) и ВM = у.
Применим теорему Пифагора: d₁²=(х–1)²+у².
Далее, расстояние от точки M(x; y) до прямой x=8 равно
d₂=|8–х|.
По условию задачи
5·d₁ = d₂ или 25·d₁² = d₂².
Получим уравнение:
25·((х–1)²+у²) = (8–х)².
Упростим уравнение:
25·x²–50·x+25+25·y²–x²+16·x=64
24·x²–34·x+25·y²=39.
Пошаговое объяснение:
1) -3. 3/4 + 1. 2/15 = -3. 45/60 + 1. 8/60 = -2. 37/60
2) -2. 37/60 : 2,4 = -2. 37/60 : 2. 4/10 = -157/60 : 24/10 = -157/60 * 10/24 = -157/6 * 1/24 = -157/144
Это числитель 1 дроби
3) -157/144 : 5. 5/12 =
-157/144 : 65/12 = -157/144 * 12/65 = -157/12 * 1/65 = -157/780
Это результат 1 дроби
4) 1,35 - 4,25 = -2,9
5) -2,9 : 6 = -2. 9/10 : 6 =
-29/10 * 1/6 = -29/60
Это числитель 2 дроби
6) 3,75 * 0,2 = 0,75
7) 3 : 0,35 = 3 : 35/100 = 3 : 7/20 = 3 * 20/7 = 60/7 = 8. 4/7
8) -(0,75 + 8. 4/7) = -(75/100 + 8. 4/7) = -(3/4 + 8. 4/7) = -(21/28 + 8. 16/28) = -21/28 - 8. 16/28 = -8. 37/28 = -9. 9/28
Это знаменатель 2 дроби
9) -29/60 : (-9. 9/28) =
-29/60 : (-261/28) = -29/60 * (-28/261) = -1/15 * (-7/9) = 7/135
Это результат 2 дроби
10) -157/780 + 7/135 =
-1413/7020 + 364/7020 =
-1049/7020
Это результат примера