
ответ:Изображение обыкновенных дробей и смешанных чисел на координатном луче.
Для того чтобы изобразить дробь на координатном луче нужно сначала посмотреть на знаменатель. Знаменатель показывает на сколько равных частей нужно разделить единичный отрезок.
Пошаговое объяснение: Пример: дробь 3/4 нужно от нуля до 1 разделить единичный отрезок на 4 равные части. От 0 вправо вы отсчитываете 4 клеточки и ставите цифру 1. Между 0 и 1будут дроби 1/4, 2/4,3/4 и 4/4(это 1). Теперь нам нужна дробь 3/4 поэтому от нуля вправо на три клеточки и поставьте точку. Это и будет дробь 3/4.
В Вашем же случае: 1/6 – мы определяем отрезок от нуля до единицы от нуля шесть клеточек и ставим точку. На шестой точке внизу ставим единицу. На самой первой чёрточке ставим ноль ещё одну клетку, и сверху ставим дробь 1/6. Желательно рисуем луч 10 см., так будет проще и легче. Здесь можно же начертить второй отрезок. От единицы до двойки должно быть шесть клеточек! После единицы-же*отрезка отшагаем одну клетку и на первой же чёрточке пишем 1 целое*целое не надо писать 1/6.
Дальше рисуем другой луч от первой чёрточки-нуля три чёрточки и ставим точку на третей клеточке и внизу ставим единицу. Ставим точку на Нуле и на Единице. От нуля клетку и на первой чёрточке-же сверху пишем 1/3. После этого, на этом же луче, отступаем ещё одну клеточку, и пишем 2/3.
Рисуем новый луч. Делаем отрезок от нуля до единицы 2-к клетки и пишем нуль на первой чёрточке и единицу на второй клеточке. И делаем ещё один отрезок по две клетки. Пишем 1*целое 1/2.
Если же будет 2*целых и 3/7 то мы делаем три отрезка. После отрезков чёрточки не рисуем. И так: рисуем от 0 – три отрезка по семь клеток. И отступаем от второго отрезка три клетки и на третьей клетке сверху пишем 2*целых 3/7(это я например написала).
Если же с буквами то сверху–где мы пишем дроби, можно написать буквы.
Пошаговое объяснение:
1) область определения функции: x ∈ R
2) проверим на четность:
y(-x) = -2x/(1 + x²) = -y(x) - функция нечетная
3) функция не периодическая
4) y = 0 только при х = 0, значит, точка пересечения с осями только (0; 0)
5) функция непрерывна
6) y' = (2(1 + x²) - 4x²)/(1+x²)² = (2 - 2x²)/(1 + x²)² = 0
2 - 2x² = 0
2x² = 2
x = -1 или x = 1
y'' = (4x³ - 12x)/(1+x²)³
y''(-1) > 0
y''(1) < 0
x = -1 - точка минимума
x = 1 - точка максимума
7) находим асимптоты:
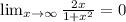
x = 0 - асимптота
найдем наклонные асимптоты:
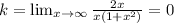
больше нет асимптот
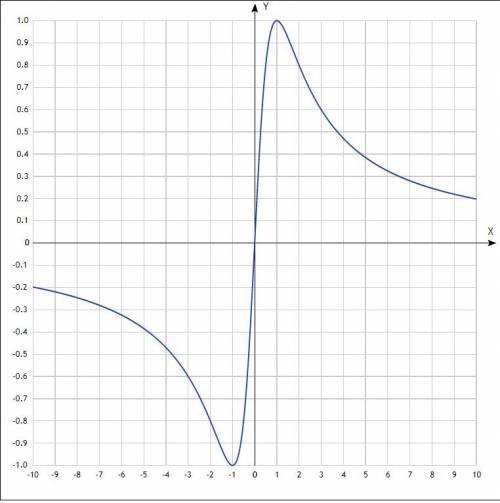
это просто