Задайте формулой функцию, если известно, что ее график параллелен графику функции y = -2,0 x + 7 и проходит через точку пересечения графиков функций y = x − 2 и y =-3x +18 .

👇

Увидеть ответ

Ответ:

looolll2k17

04.03.2021

уравнение пряммой будем искать в виде y=kx+b

так как данная пряммая параллельная пряммой y=-6x, а у паралельных прямых угловые коэффициенты равны, то k=-6

и уравнение пряммой запишется так y=-6x+b

Далее, так как она проходит через точку K (1;-10), то справедливо равенство

-10=-6*1+b;

-10=-6+b;

-10+6=b;-4=b;

b=-4

а значит уравнение искомой пряммой имеет вид y=-6x-4

Пошаговое объяснение:

4,4(21 оценок)

Открыть все ответы

Ответ:

MariaStredinina

04.03.2021

Пошаговое объяснение:

самое простое объяснение

конечная десятичная дробь это дробь или смешанное число , у которой в знаменателе 10 , 100 , 1000 , 10000 и т.д. а в числителе число (целое)

например 0,5; 3,15; 10,125 и т.д.

а вот бесконечная дробь, это дробь у которой числитель "не кончается"

например 0,555555 или 3,156666666 или 10,1257377777

мы знаем, что десятичные дроби получаются из простых путем деления числителя на знаменатель.

так вот, если числитель нацело делится на знаменатель, то будет конечная дробь, если же делить можно бесконечно и нацело не поделится, тогда и будет бесконечная дробь..

например 1/2 : 1 делим на 2 получаем 0,5 поделилось нацело

7/9 7 делим на 9 и делить можем хоть 100 лет, а конечного результата не получим. это и будет бесконечная дробь 0,7777777

4,8(6 оценок)

Ответ:

Msскрытность

04.03.2021

Пошаговое объяснение:

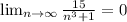$\lim_{n \to \infty} \frac{15}{n^3+1}=0$ . Докажем это.

По определению предела, для всякого положительного ε найдется номер N, что для всех номеров n, бОльших N, верно, что 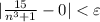$| \frac{15}{n^3+1}-0|< \varepsilon$ .

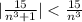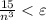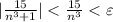Заметим, что $| \frac{15}{n^3+1}|< \frac{15}{n^3}$ для всякого натурального n. Тогда, если $\frac{15}{n^3}< \varepsilon$ , или (решая неравенство относительно n) $n \sqrt[3]{\frac{15}{\varepsilon}}$ , то, взяв в качестве N целую часть числа $\sqrt[3]{\frac{15}{\varepsilon}}$ , получим, что $| \frac{15}{n^3+1}|< \frac{15}{n^3} < \varepsilon$ . 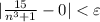Резюмируя: научились для всякого положительного ε находить номер N (в качестве N можно взять целую часть числа $\sqrt[3]{\frac{15}{\varepsilon}}$ ), что для всех номеров n, бОльших N, выполняется неравенство $| \frac{15}{n^3+1}-0|< \varepsilon$ . А это и значит, что предел равен нулю.

Интуитивно это можно объяснить так: увеличивая номер n, получаем все меньшее и меньшее число, причем оно всегда больше нуля, но его можно сделать очень маленьким.

Аналогично, докажем, что 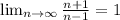$\lim_{n \to \infty} \frac{n+1}{n-1}=1$

По определению предела, для всякого положительного ε найдется номер N, что для всех номеров n, бОльших N, верно, что 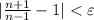$| \frac{n+1}{n-1}-1|< \varepsilon$ .

Заметим, что 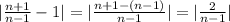$|\frac{n+1}{n-1}-1|=|\frac{n+1-(n-1)}{n-1}|=|\frac{2}{n-1}|$ . Тогда, если 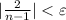$|\frac{2}{n-1}|< \varepsilon$ , или (решая неравенство относительно n) 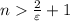$n \frac{2}{\varepsilon}+1$ , то, взяв в качестве N целую часть числа 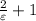$\frac{2}{\varepsilon}+1$ , получим, что 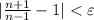$| \frac{n+1}{n-1}-1|< \varepsilon$ . Резюмируя: научились для всякого положительного ε находить номер N (в качестве N можно взять целую часть числа 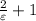$\frac{2}{\varepsilon}+1$ ), что для всех номеров n, бОльших N, выполняется неравенство 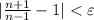$| \frac{n+1}{n-1}-1|< \varepsilon$ . А это и значит, что предел равен единице.