(3/14; 1 3/7).
Пошаговое объяснение:
{2x-y+1=0,
{8x+3y-6=0;
{у = 2х + 1,
{8x+3y-6=0;
{у = 2х + 1,
{8x+3•(2х + 1) - 6=0;
{у = 2х + 1,
{8x+6х + 3 - 6=0;
{у = 2х + 1,
{14х - 3=0;
{у = 2х + 1,
{14х = 3;
{у = 2х + 1,
{х = 3/14;
{у = 2•3/14 + 1,
{х = 3/14;
{у = 1 3/7,
{х = 3/14;
(3/14; 1 3/7) - координаты точки пересечения прямых.
Проверка:
1) 2•3/14 - 1 3/7 + 1 = 0,
3/7 - 1 3/7 + 1 = 0
0=0 - верно, точка лежит на первой прямой.
2) 8•3/14 + 3•1 3/7 - 6 = 0
12/7 + 3 9/7 - 6 = 0
6 - 6 = 0
0=0 - верно, точка лежит и на второй прямой.
Пошаговое объяснение:
воспользуемся предельным признаком сравнения
для этого для нашей функции f(x) найдем удобную функцию g(x), сходимость интеграла которой известна, и найдем
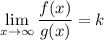
и тогда, если к≠ 0, то несобственные интегралы от этих функций функции ведут себя одинаково
как правило в качестве g(x) выбирают степенную функцию, т.к. известно, что
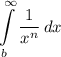сходится при n > 1, и расходится при n ≤ 1
итак наша функция f(x) эквивалентна функции g(x)
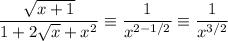
теперь предел
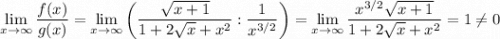
следовательно несобственный интеграл f(x) ведет себя также как несобственный интеграл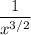 
, т.е сходится.
1) 5*3 = 15 (человеко-дней) - у 1-ой бригады
2) 6*4 = 24 (человеко-дней) - у 2-ой бригады
3) 15+24=39 (человеко-дней) - всего
4) 3900:39=100(руб.) - стоит 1 человеко-день
5) 100*15 = 1500 (руб) - получит 1-я бригада