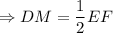45 - ( х - 16 ) = 23
45 - х + 16 = 23
61 - х = 23
- х + 61 = 23
- х + 61 - 61 = 23 - 61
- х = - 38
- х - 38
=
- 1 - 1
х = 38
Пошаговое объяснение:
1 ) для начала нужно раскрыть скобки.
2 ) сложить числа.
3 ) переставить члены уравнения.
4 ) вычесть 61 из обеих частей уравнения.
5 ) упростить.
6 ) разделить обе части уравнения на один и тот же член.
7 ) упростить.
ответ : 38.
Пошаговое объяснение:
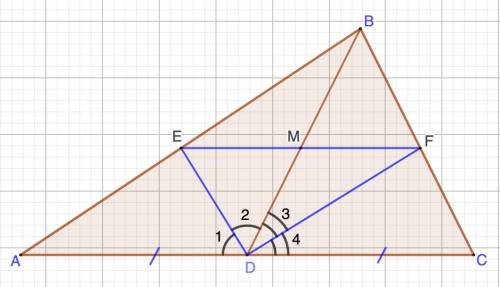
Дано: ΔАВС.
AD = DC;
DE u DF-биссектрисы.
Доказать: 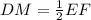
Доказательство:
1. Рассмотрим ΔDEF.
∠1 + ∠2 +∠3 +∠4 = 180° (∠ADC - развернутый)
∠1 = ∠2; ∠3 = ∠4 (DE u DF-биссектрисы)
⇒ ∠2 + ∠3 = 90°
⇒ ΔDEF - прямоугольный.
2. Рассмотрим ΔABD.
DE - биссектриса.
Биссектриса угла треугольника делит противоположную сторону в отношении, равном отношению двух прилежащих сторон .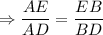 или
или 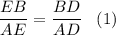
3. Рассмотрим ΔDBC.
DF - биссектриса.
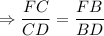 или
или 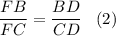
4. AD = CD (по условию)
В равенствах (1) и (2) правые части равны, ⇒ равны и левые, то есть:

⇒ EF || AC
5. Рассмотрим ΔEBM и ΔABD.
EM || AD
Если две стороны треугольника пересекает прямая, параллельная третьей стороне, то она отсекает треугольник, подобный данному.⇒ ΔEBM ~ ΔABD , тогда
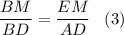
6. Рассмотрим ΔMBF и ΔDBC.
MF || DC
⇒ ΔMBF ~ ΔDBC.
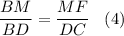
В равенствах (3) и (4) левые части равны, ⇒ равны и правые:
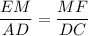
Так как AD = DC ⇒ EM = MF.
7. Рассмотрим ΔEFD - прямоугольный.
EM = MF ⇒ DM - медиана.
Медиана, проведенная из вершины прямого угла к гипотенузе равна ее половине.