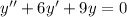
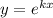 .
.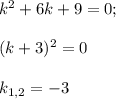
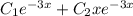
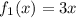 и
и 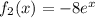
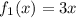
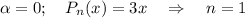
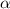 с корнями характеристического уравнения, и, принимая во внимания, что n=1, частное решение будем искать в виде.
с корнями характеристического уравнения, и, принимая во внимания, что n=1, частное решение будем искать в виде.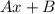
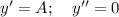 , подставим в исходное уравнение без функции
, подставим в исходное уравнение без функции 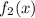 .
.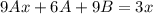
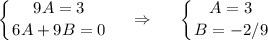
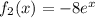
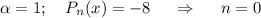
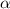 с корнями характеристического уравнения и принимая во внимая, что n=0, частное решение будем искать в следующем виде:
с корнями характеристического уравнения и принимая во внимая, что n=0, частное решение будем искать в следующем виде: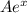
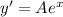 и
и 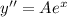
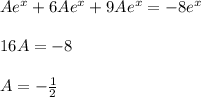
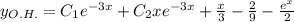
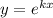 .
.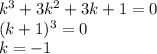
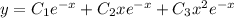
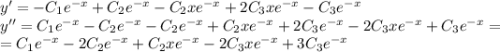
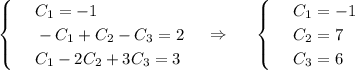
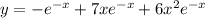
Выразите числа 5, 30 и 55, используя четыре цифры 5, знаки арифметических действий и скобки.
Задача № 2
В гимназии 33 учебных кабинета, в 2/3 кабинетах стоят по 12 парт, в остальных по 13.
Около каждой парты стоит по 2 стула. 50% всех стульев имеют по 3 ножки, остальные по 4.
Каждая парта, кроме 7, имеет по 4 ножки, а эти 7 парт по 6.
Столько всего ножек у парт и стульев в учебных кабинетах гимназии?
Задача № 3
Нюша , Бараш, Копатыч и Лосяш играли с мячами синим, зелёным, жёлтым и красным.
Каким из мячей играл каждый из них, если мяч Бараша не синий, у Нюши не синий и не красный, а у Копатыча желтый мяч?
Задача № 4
В сказочном озере плавает сказочная лилия. Эта лилия за сутки вдвое увеличивает свои размеры и полностью заполняет озеро за 137 суток.
За какое время заполнят озеро две сказочные лилии?
Задача № 5
Задуманное число добавили к числу, большему его на единицу.
Затем из суммы вычли число, на единицу меньшее задуманного.
В итоге получилось 23. Какое число было задумано?
Задача № 6
Какое наименьшее 10-значное число можно получить, по-разному записывая
шесть чисел 315, 41, 6, 7, 63 и 2 одно за другим?
Задача № 7
Две бутылки A и B заполнены водой. Сначала 1/4 воды из A перелили в B , а затем 1/3 воды из B перелили в A, после чего количество воды в них сравнялось.
Найдите первоначальное отношение количества воды в этих бутылках.
Задача № 8
В некотором месяце три воскресенья пришлись на чётные числа.
Каким днём недели могло быть 22 число этого месяца?
Задача № 9
Оттолкнувшись левой ногой, Кенгуру прыгает на 2 метра, правой – на 4, а обеими – на 7.
Какое наименьшее число таких прыжков нужно сделать, чтобы набрать в точности 300 метров?
Задача № 10
Найдите натуральное число N , для которого N+53 и N-36 –полные квадраты.
Задача № 11
Из квадрата со стороной 100 вырезали квадрат со стороной 80. Оставшийся кусок разрезали на единичные квадратики (это можно сделать), из которых Павел хочет сложить новый квадрат. Чему будет равна его сторона?
Задача № 12
Девочка заменила каждую букву в своём имени её номером в русском алфавите
и получила 2011533.
Как её зовут?
Задача № 13
В букете 11 цветов, причём 5 из них – красные, а 6 – розы.
Какое число белых гвоздик может быть в букете?
Задача № 14
Какое наименьшее 10-значное число можно получить, по-разному записывая шесть чисел 316, 21, 6, 7, 83 и 3 одно за другим?
Задача № 15
В некотором месяце три понедельника пришлись на нечётные числа.
Каким днём недели могло быть 21 число этого месяца?