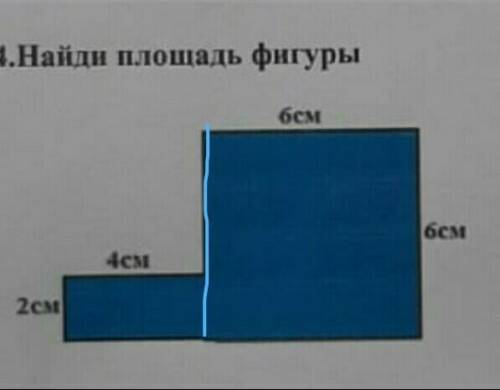
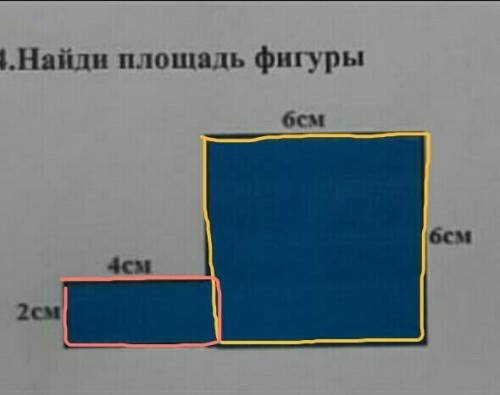
Разделим фигуру на 2 следующие : квадрат и прямоугольник.
===================================================→ Мы знаем, что по свойству у квадрата все сторны равны (здесь по 6 см каждая). Соответственно площадь квадрата равна :
S = a² = 6² = 6 * 6 = 36 (см²).
===================================================→ Мы знаем, что по свойству у прямоугольника противолежащие стороны равны (по 4 (см) и по 2 (см) ). Соответственно площадь прямоугольника равна :
S = a * b = 4 * 2 = 8 (см²).
===================================================Мы знаем, что чтобы найти площадь какой-либо фигуры, нужно сложить площади её частей (квадрата и прямоугольника). Т.е. площадь фигуры равна :
S = S(квадрата) + S(прямоугольника) = 36 + 8 = 44 (см²).
===================================================
б)4,121212121212…
в)5,1666666…
г)8,08666666…
д)13,11090909090909…
(вроде так)
Особое место среди всех дробей занимают периодические дроби – бесконечные числа, в то же время считающиеся рациональными, поскольку они могут быть трансформированы в обыкновенные дроби. Например: 6,27777777..., записывается в виде: 6,2(7), период помещается в скобки (7 в периоде). Периодическую бесконечную десятичную дробь можно перевести в обыкновенную дробь.
Периодические дроби делятся на чистые и смешанные, и они подчиняются разным алгоритмам перевода. У чистых периодических дробей период расположен сразу после запятой. В смешанных периодических дробях между запятой, отделяющей целую часть от дробной, и периодом могут присутствовать другие цифры.
Примеры записи периодических дробей:
1/6 = 0.1(6) = 0.1666...
1/7 = 0.(142857) = 0.142857...