Найдем начала общее решение соответствующего однородного дифференциального уравнения
(*)
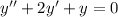Воспользовавшись заменой Эйлера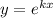 
, мы получим характеристическое уравнение
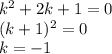
Общее решение уравнения (*)
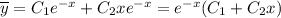
Далее нужно найти частное решение. Рассмотрим функцию:
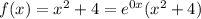
Здесь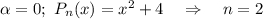 
Сравнивая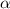 
с корнями характеристического уравнения и, принимая во внимая, что 
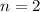частное решение будем искать в виде
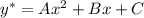
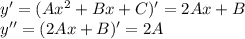
Подставляем все это в исходное дифференциальное уравнение
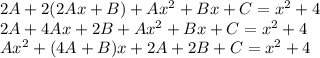
Приравниваем коэффициенты при степени x
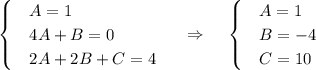
Частное решение: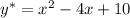 
Общее решение линейного неоднородного дифференциального уравнения:
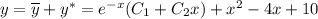
В треугольнике АДС СД=АД (в ромбе ВСЕ стороны равны)
AD^2=CD^2+AD^2-2*CD*AD*cos (135)
AD^2=9+9-2*3*3 cos(180-45)=18-18*(cos(45))
AD=√(18-18*(cos(45))
cos(45)=√2/2