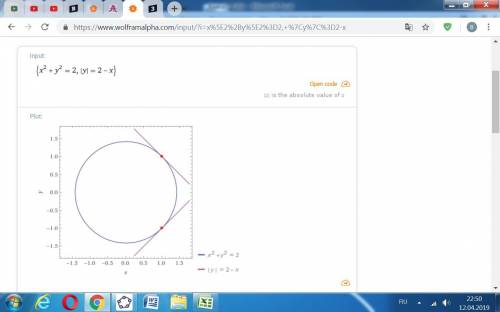
Заданная система уравнений х^2 + у^2 = 2, х+|y| = a графически представляет собой 3 фигуры:
- окружность х^2 + у^2 = 2,
- прямую у = -х + а,
- прямую у = х - а.
Эти прямые взаимно перпендикулярны и чтобы было 2 решения, они должны касаться окружности каждая в одной точке.
Радиусы в точку касания параллельны прямым, но так как они идут из начала координат, то их уравнения у = х и у = -х.
Возьмём у = х и у = -х + а и приравняем: 2х = а, х =а/2, но и у = х = а/2.
Подставим ув уравнение окружности: (а²/4) + (а²/4) = 2, 2а² = 8,
а² = 8/2 = 4. Отсюда а = +-2.
ответ: наибольшее значение параметра а равно 2.
6823+6823=13646
объяснение:при сложении цифр первого разряда Н+Н=О, то есть О- чёрное число.
При сложении цифр чёрного разряда О+О=МН.Так как сумма О+О - двухзначное число, значит О больше 5.
Чётные цифры которые больше 5,это 6 или 8.
Допустим, что О=8, тогда Н=4, а 8+8 =М4, что не возможно при любых М.
Допустим, что О=6, тогда Н=3, а 6+6=М3, что возможно при М=1.
Наше выражение принимает вид:
6ДИЗ+6ДИЗ=136Г6.
Д+Д дают сумму, которая заканчивается на 6,значит Д может быть ровно 8:
68ИЗ+68ИЗ=136Г6.
И+И=Г, И не может быть ровно 1,так как М=1, и Г- чётное число, значит Г=4, И=2, получаем:
6823+6823=13646
Пошаговое объяснение:
4р. 29к.
Пошаговое объяснение:
25р. 3к. - 12р. 16к. = 12р. 87к
12р. 87к. : 3 = 4р 29к