Вычислить площадь фигуры, ограниченной линиями y = х² + 4x + 3 и y = x + 3. Построить график , нужна в решении.

👇

Увидеть ответ

Ответ:

Адема12345

07.10.2022

9/2

Пошаговое объяснение:

Сначала чертим графики

y = х² + 4x + 3

Выделим полный квадрат х² + 4x + 3 = (х² +2*2х +4) -4 +3 = (х+2)² -1

значит, берем известный график функции у = х²,

смещаем его на -2 по оси ОХ и на -1 по оси ОУ.

y = x + 3

берем известный график у = х и смещаем его на -3 по оси ОХ.

Вот мы получили нужную нам фигуру.

Теперь по формуле Ньютона - Лейбница вычислим определенный интеграл, что и будет площадью фигуры

$\displaystyle S=\int\limits^a_b {\bigg (y_1(x) -y_2(x)\bigg )} \, dx$ , где

х ∈ [a; b] ; за у₁(х) принимают функцию, график которой лежит "выше" на отрезке [a; b]

Для нашего случая

$\displaystyle S=\int\limits^0_{-3} {\bigg ((x+3)-(x^2+4x+3)\bigg )} \, dx =\int\limits^0_{-3} { (-x^2-3x)} \, dx =\\\\\\=\bigg (-\frac{x^3}{3} \bigg ) \bigg |_{-3}^0-3\frac{x^2}{2} \bigg |_{-3}^0=-9+\frac{27}{2} =\boldsymbol {\frac{9}{2} }$

Вычислить площадь фигуры, ограниченной линиями y = х² + 4x + 3 и y = x + 3. Построить график , нужна

4,8(5 оценок)

Открыть все ответы

Ответ:

elvinabilalova

07.10.2022

Пошаговое объяснение:

1)Находим объем всего многогранника по данным размерам

V= 3 * 3 * 1=9 см3, затем считаем объем недостающей части

V= 1 * 1* 1= 1 см3

объем многогранника изображенного на рисунке:

V= 9 - 1 = 8 см3

2) ответ: боковое ребро 13 см

V=1/3S*h

S=3V/h=600/12=50

S=a²=50

Обозначим за b боковую сторону и найдем по т. Пифагора:

b=√h²+(d/2)², d - диагональ квадрата

d=a√2

d/2=a√2/2

(d/2)²=a²/2

b=√144+50/2=√169=13 см

3) Sос.с = 10 cм2, Sосн.= 5см2 П- пи

S ос.с= h*d d=2r 10=h*2r r= 10/2h = 5/h

S =Пr^2 5=Пr^2 П(5/h)^2 =5 5П/h^2=1

h= √(1/5П)^-1 =√5П м

4)V₁ = 1/3πR₁²Н₁

V₂ = 1/3π(3R₁)²Н₁/2= 1/3π9R₁²Н₁/2=1,5πR₁²Н₁ м3

V=1/3 Sосн.* h

Sосн.= 3 * 4 = 12 см2

V=1/3*12*6=24 cм3

4,7(100 оценок)

Ответ:

annkhanenko23

07.10.2022

Задание 1. Всего количество чисел от 10 до 60 - 60-9=51. Среди них, количество чисел, делящихся на 4 равно 13 (12;16;20;24;28;32;36;40;44;48;52;56;60)

Искомая вероятность : P=13/51 ≈ 0.25

Задание 2. Выбрать один белый шар можно

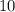а два черных шара - 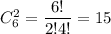$C^2_6= \dfrac{6!}{2!4!} =15$ По правилу произведения, вынуть один белый шар и два черных шара можно кол-во благоприятных событий)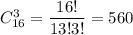

Количество все возможных событий: $C^3_{16}= \dfrac{16!}{13!3!}= 560$

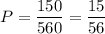
Искомая вероятность: $P= \dfrac{150}{560}= \dfrac{15}{56}$

Задание 3. Выбрать одного мужчину можно а трёх женщин - $C^3_{10}= \dfrac{10!}{3!7!}= 120$ И тогда выбрать делегацию из четырёх человек(1 мужчина и 3 женщин) можно

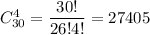
Количество все возможных событий: $C^4_{30}= \dfrac{30!}{26!4!}= 27405$

Искомая вероятность $P= \dfrac{2400}{27405} = \dfrac{160}{1827}\approx 0.09$

Задание 4. Число испытаний: n=3, вероятность успеха - 0,8, вероятность неудачи - q=1-0.8=0.2. Искомая вероятность по формуле Бернулли:

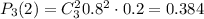
$P_3(2)=C^2_30.8^2\cdot0.2=0.384$

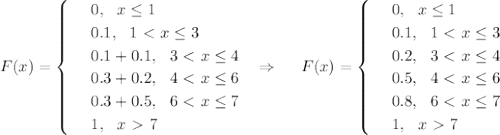
Задание 5. $F(x)=\begin{cases}
 & \text{ } 0,~~ x \leq 1 \\ 
 & \text{ } 0.1,~~1\ \textless \ x \leq 3 \\ 
 & \text{ } 0.1+0.1,~~3\ \textless \ x \leq 4 \\ 
 & \text{ } 0.3+0.2,~~4\ \textless \ x \leq 6 \\ 
 & \text{ } 0.3+0.5,~~6\ \textless \ x \leq 7 \\ 
 & \text{ } 1,~~x\ \textgreater \ 7 
\end{cases}~~\Rightarrow~~~~F(x)=\begin{cases}
 & \text{ } 0,~~ x \leq 1 \\ 
 & \text{ } 0.1,~~1\ \textless \ x \leq 3 \\ 
 & \text{ } 0.2,~~3\ \textless \ x \leq 4 \\ 
 & \text{ } 0.5,~~4\ \textless \ x \leq 6 \\ 
 & \text{ } 0.8,~~6\ \textless \ x \leq 7 \\ 
 & \text{ } 1,~~x\ \textgreater \ 7 
\end{cases}$

Задание 6. В таблице вероятности сумма вероятностей должна равняться 1, то есть

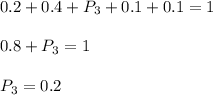
$0.2+0.4+P_3+0.1+0.1=1\\ \\ 0.8+P_3=1\\ \\ P_3=0.2$

Вычислим математическое ожидание по определению $M(X)=\displaystyle \sum x_ip_i$

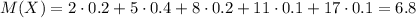
$M(X)=2\cdot0.2+5\cdot0.4+8\cdot0.2+11\cdot0.1+17\cdot0.1=6.8$

Дисперсия:
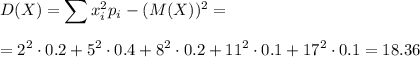
$D(X)=\displaystyle \sum x_i^2p_i-(M(X))^2=\\ \\ =2^2\cdot0.2+5^2\cdot0.4+8^2\cdot0.2+11^2\cdot0.1+17^2\cdot0.1=18.36$

Среднее квадратическое отклонение σ(x).

$\sigma (X)= \sqrt{D(X)}= \sqrt{18.36} \approx 4.285$
1.какова вероятность того, что наудачу выбранное число от 10 до 60 кратно 4? 2.из ящика, в котором 1