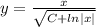
или так
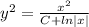
Пошаговое объяснение:
Найти общее решение дифференциального уравнения первого порядка.
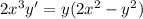
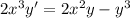
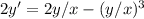
Получили однородное дифференциальное уравнение
Проводим замену приводящую к уравнению с разделяющимися переменными
у = xt(x) y’ = t + xt’
2(t + xt’) = 2t – t³
2xt’ = – t³
2t’/t³ = -1/x
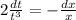
Интегрируем обе части уравнения
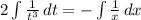
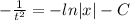
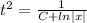
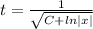
Находим переменную у
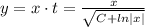
Получили общее решение диф. уравнения