ответ: 0,664 - вызов будет принят.
Пошаговое объяснение:
Вероятность первого вызова: p₁ = 0.2 - принят и q₁ = 1 - 0.2 = 0.8 - пропущен. Аналогично для следующих вызовов: p₂ = 0.3, q₂ = 0.7 и p₃ = 0.4, q₃ = 0.6,
Вероятность принять вызов за три попытки - P(A).
Событие Р(А) - первый "да" ИЛИ первый "нет" И второй "да" ИЛИ первый "нет" И второй "нет" И третий "да".
Вероятности событий ИЛИ - равна сумме вероятностей каждого.
Вероятности событий И - равны произведению вероятностей каждого.
Р(А) = p₁ + q₁*p₂ + q₁*q₂*p₃
Р(А) = 0,2 + 0,8*0,3 + 0,8*0,7*0,4.
Р(А) = 0,2 + 0,24 + 0,224 = 0,664 - вызов принят - ОТВЕТ
ИЛИ
Вероятность противоположного события Q(A) - вызов не принят за три вызова - И первый "нет" И второй "нет" И третий "нет"
Q(A) = q₁ * q₂ * q₃ = 0.8*0.7*0.6 = 0.336 - не принят.
Р(А) = 1 - Q(A) = 1 - 0.336 = 0.664 - принят.
ответ: 0,664 - вызов будет принят.
Пошаговое объяснение:
Вероятность первого вызова: p₁ = 0.2 - принят и q₁ = 1 - 0.2 = 0.8 - пропущен. Аналогично для следующих вызовов: p₂ = 0.3, q₂ = 0.7 и p₃ = 0.4, q₃ = 0.6,
Вероятность принять вызов за три попытки - P(A).
Событие Р(А) - первый "да" ИЛИ первый "нет" И второй "да" ИЛИ первый "нет" И второй "нет" И третий "да".
Вероятности событий ИЛИ - равна сумме вероятностей каждого.
Вероятности событий И - равны произведению вероятностей каждого.
Р(А) = p₁ + q₁*p₂ + q₁*q₂*p₃
Р(А) = 0,2 + 0,8*0,3 + 0,8*0,7*0,4.
Р(А) = 0,2 + 0,24 + 0,224 = 0,664 - вызов принят - ОТВЕТ
ИЛИ
Вероятность противоположного события Q(A) - вызов не принят за три вызова - И первый "нет" И второй "нет" И третий "нет"
Q(A) = q₁ * q₂ * q₃ = 0.8*0.7*0.6 = 0.336 - не принят.
Р(А) = 1 - Q(A) = 1 - 0.336 = 0.664 - принят.
Дано:
∠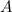
Выяснить: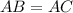 или
или 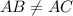 .
.
Решение.
1) Рассмотрим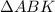 и
и 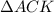 .
.
У них:
∠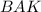 =∠
=∠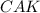 , как половинки ∠
, как половинки ∠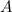 ;
;
∠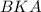 = ∠
= ∠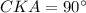 как углы, образованные
как углы, образованные
перпендикулярными прямыми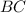 и
и 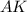 ;
;
Таким образом, сторона и два прилежащих к ней угла одного треугольника равны стороне и двум прилежащих к ней углам другого треугольника, а это означает, что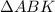 =
= 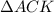 .
.
2) Из равенства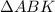 и
и 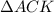 следует равенство соответственных сторон:
следует равенство соответственных сторон: 
и соответственных углов ∠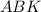 =∠
=∠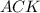 .
.
=> Δ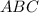 - равнобедренный.
- равнобедренный.
ответ: да, можно.