Найдем сначала наибольшее и наименьшее значения функции
y=(x+1)²(5-x). В силу того, что функция извлечения корня третьей степени монотонно возрастает, достаточно будет затем умножить найденные значения на 2, извлечь корень третьей степени из получившихся чисел, после чего вычесть из них 2.
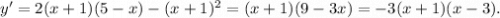
Внутри интервала (-3;3) лежит один из нулей производной - это x=-1. Найдем значения функции в точках -3; 3 (концах отрезка) и в точке -1:
y(-3)=y(3)=32 - наибольшее значение; y(-1)=0 - наименьшее значение.
Осталось с получившимися числами проделать указанные операции - умножить на 2, извлечь корень третьей степени и вычесть 2:
![\sqrt[3]{2\cdot 32}-2=4-2=2;\ \sqrt[3]{2\cdot 0}-2=-2.](/tpl/images/2074/3094/1128c.png)
ответ: наибольшее значение равно 2 и достигается на концах отрезка, наименьшее значение равно минус 2 и достигается в точке минус 1.
Геометрическое решение.
Применим перенос одного из отрезков так, чтобы их концы соединились.
Перенесём отрезок AD1 точкой D1 в точку D.
При этом точка А перейдёт в точку А2.
Получим треугольник DA2F1 с искомым углом D. Находим длины его сторон.
Сначала определим их проекции на основание.
AD = 1 + 2*(1*cos 60º) = 1 + 2*(1*(1/2)) = 2.
Тогда AD1 = √(2² + 1²) = √(4 + 1) = √5.
Находим DF = 2*(1*cos 30º) = 2*(1*(√3/2)) = √3.
Тогда DF1 = √((√3)² + 1²) = √(3 + 1) = √4 = 2.
И последний отрезок A2F1. Он равен:
A2F1= √(2² + 1²) = √(4 + 1) = √5.
Применим теорему косинусов.
cos D = (2² + (√5)² - (√5)²) / (2*2*√5) = 4/(4*√5) = √5/5 ≈ 0,4472.
Угол D = arccos(√5/5) = 1,1071 радиан или 63,435 градуса.