1012036
Пошаговое объяснение:
Нули модулей — x = 1, 2, 3, ..., 2012. Если x < 1006, то есть меньше половины модулей раскрылось с плюсом, то в итоге коэффициент перед x будет отрицательный, при x < 1006 функция убывает. Если x ≥ 1007, то больше половины модулей раскрылось с плюсом, то коэффициент перед x будет положительный, при x ≥ 1007 функция возрастает. Значит, при 1006 ≤ x < 1007 функция достигает своего минимума. При данных x получим:
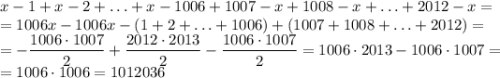
На промежутке 1006 ≤ x < 1007 значение функции равно 1012036. С учётом предыдущих рассуждений, оно наименьшее.
Пусть, горизонтальный прямоугольник уже размещен. Тогда, искомая вероятность - вероятность того, что вертикальный прямоугольник будет пересекать горизонтальный. Заметим, что пересечение возможно только в одной клетке.
Рассмотрим две ситуации.
1. Горизонтальный прямоугольник лежит в крайней (верхней или нижней) строке. Так как всего строк 4, то это может произойти с вероятностью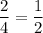 . Найдем общее число возможных расположений вертикального прямоугольника и число расположений, при которых он пересекается с горизонтальным.
. Найдем общее число возможных расположений вертикального прямоугольника и число расположений, при которых он пересекается с горизонтальным.
Так как высота вертикального прямоугольника 3, а высота исходного прямоугольника 4, то в каждом столбце вертикальный прямоугольник моет располагаться двумя Таким образом, общее число расположений вертикального прямоугольника равно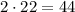 .
.
Вертикальный прямоугольник будет пересекаться с горизонтальным в 3 случаях: если он будет располагаться в одном из столбцов, через которые проходит горизонтальный прямоугольник и примыкать к соответствующей крайней строке. Значит, число расположений вертикального прямоугольника, при которых он пересекается с горизонтальным, равно 3.
Учитывая вероятность появления этой ситуации, получим, что пересечение в этой ситуации происходит с вероятностью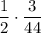 .
.
2. Горизонтальный прямоугольник не лежит в крайней строке. Таких строк тоже 2, значит произойти это может также с вероятностью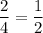 .
.
Общее число расположений вертикального прямоугольника по-прежнему равно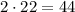 .
.
Вертикальный прямоугольник будет пересекаться с горизонтальным, если он будет располагаться в одном из столбцов, через которые проходит горизонтальный прямоугольник, причем располагаться в конкретном столбце он может любым из двух возможных Значит, число расположений вертикального прямоугольника, при которых он пересекается с горизонтальным, равно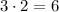 .
.
Учитывая вероятность появления этой ситуации, получим, что пересечение в этой ситуации происходит с вероятностью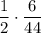 .
.
Рассмотренные ситуации не совместны, так как горизонтальный прямоугольник не может располагаться в двух строках одновременно. Значит, соответствующие вероятности необходимо складывать:
ответ: 9/88