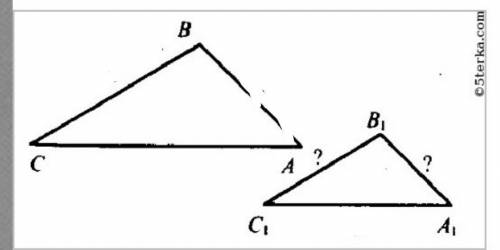
1 задача.
Треугольник ABC и A1B1C1 подобны, следовательно;
AB/A1B1=AC/A1C1=BC/B1C1
Возьмём большую сторону A1C1.
Значит выходит:
10/A1B1=15/12=12/B1C1 отсюда:
A1B1=10*12/15=8;B1C1=12*12/15=9.6
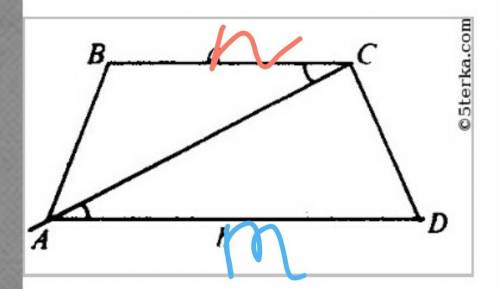
2 задача.
Треугольники ABC и ACD подобны;AD=m и BC=n.
Два треугольника подобны значит:AB/DC=BC/AC=AC/AD
AC²=AD*BC(свойства пропорции)
т.е. АС²=m*n
3 задача.
прямая пересекающия стороны в точках M и N
В треугольнике ABC и MNC;угол С общий.
угол М=угол А(потому что АВ||a)
Значит треугольник АВС и МNC подобны (по двух углам),отсюда:
BC/NC=AB/MN=AC/MC=4+5/5
Вот что выходит:AB/MN=9/5;BC/NC=9/5;AC/MC=9/5
MN=5/9AB=1.4×5=7см
NC=5/9BC=2×5=10см
MC=5/9AC=1.7×5=8.5см

Пусть скорость течения реки равна х км/ч. Скорость лодки, движущейся по течению реки равна (20 + х) км/ч, а скорость лодки, движущейся против течения реки - (20 - х) км/ч. Путь пройденный первой лодкой за 1 час равно (20 + х) километров (чтобы найти пройденный путь, надо скорость умножить на время), а путь, пройденный второй лодкой за 2 часа, равен 2(20 - х) километров. Расстояние между двумя пунктами реки равно сумме расстояний пройденными лодками до их встречи и равно (20 + х + 2(20 - х)) километров или 57 км. Составим уравнение и решим его.
20 + х + 2(20 - х) = 57;
20 + x + 40 - 2x = 57;
- x + 60 = 57;
- x = 57 - 60;
- x = - 3;
x = 3 (км/ч).
ответ. 3 км/ч.
там всё легко
1) 48 : 8 = 6 (см) - другая сторона прямоугольника.
2) 48 * 6 = 288 (кв. см) - S прямоугольника
ответ : S прямоугольника - 288 кв. см.