Математика матем матем матем матем ОТВЕТ: 165. 2 см, 166.28см

❤не за что

👇

Увидеть ответ

Ответ:

denisprokopev

23.09.2022

165.2 см 166.28 см

4,7(35 оценок)

Открыть все ответы

Ответ:

dog126

23.09.2022

Пусть - длина дуги, ограничивающей искомый сектор, вырезаемый из круглого листа.

Пусть 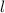- радиус круглого листа и одновременно образующая конуса (воронки).

Тогда радианная мера дуги 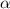$\alpha$ , ограничивающей искомый сектор равна:

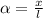$\alpha=\frac{x}{l}$ ---------(1)

Нам необходимо найти при каком объем воронки (правильного конуса)

будет наибольшим. Запишем формулу объема 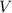конуса:

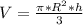$V=\frac{\pi*R^{2}*h}{3}$ --------(2)

где 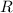- радиус основания конуса; 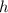- высота конуса

Поскольку длина окружности основания конуса равна , то отсюда

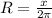$R=\frac{x}{2\pi}$ --------(3)

Высоту конуса найдем с теоремы Пифагора:

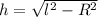$h=\sqrt{l^{2}-R^{2}}$ -------(4)

Подставим в (4) вместо 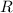выражение (3):

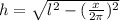$h=\sqrt{l^{2}-(\frac{x}{2\pi})^{2}}$ --------(5)

Подставим в (2) вместо 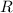и 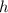соотвественно выражения (3) и (5), получим:

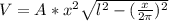$V=A*x^{2}\sqrt{l^{2}-(\frac{x}{2\pi})^{2}}$ --------(6)

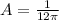
где $A=\frac{1}{12\pi}$

Очевидно, что естественной областью определения объема как функции от есть интервал:

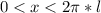$0<x<2\pi*l$ ------(7)

Продифференцируем (6) по :

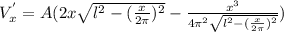$V^{'}_{x}=A(2x\sqrt{l^{2}-(\frac{x}{2\pi})^{2}}-\frac{x^{3}}{4{\pi}^{2}\sqrt{l^{2}-(\frac{x}{2\pi})^{2}}})$ , отсюда

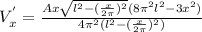$V^{'}_{x}=\frac{Ax\sqrt{l^{2}-(\frac{x}{2\pi})^{2}}(8{\pi}^{2}l^{2}-3x^{2})}{4{\pi}^{2}(l^{2}-(\frac{x}{2\pi})^{2})}$ --------(8)

Чтобы функция (6) имела на естественной области ее определения максимум или минимум, необходимо чтобы 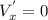$V^{'}_{x}=0$ --------(9)

Тогда из (8) и (9) получим:

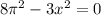$8{\pi}^2-3x^{2}=0$ , отсюда с учетом, что 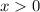, найдем критическую точку:

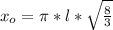$x_{o}=\pi*l*\sqrt{\frac{8}{3}}$ , или

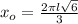
$x_{o}=\frac{2{\pi}l\sqrt{6}}{3}$

Поскольку естественной области определения (7) принадлежит только одна критическая точка 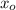$x_{o}$ и поскольку на естественной области определения функция (6) принимает только положительные значения, то критическая точка 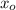$x_{o}$ - точка максимума функции (6). Другими словами, при 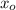$x_{o}$ объем воронки будет наибольшим.

Теперь мы можем найти радианную меру искомого сектора, для чего подставим в (1) вместо критическую точку $x_{o}$ :

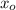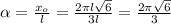
$\alpha=\frac{x_{o}}{l}=\frac{2{\pi}l\sqrt{6}}{3l}=\frac{2{\pi}\sqrt{6}}{3}$

4,5(67 оценок)

Ответ:

Biszkopt99

23.09.2022

Дано комплексное число в алгебраической форм:

$z=\frac{3}{2}-\frac{\sqrt{3}}{2}i$ --------(1)

где $i^{2}=-1$ по определению

Тогда $z^{*}$ комплексно-сопряженное числу комплексному числу :

$z^{*}=\frac{3}{2}+\frac{\sqrt{3}}{2}i$ -------(2)

( $z^{*}$ то же что у вас z с чертой!)

а)

$z+z^{*}=\frac{3}{2}-\frac{\sqrt{3}}{2}i+\frac{3}{2}+\frac{\sqrt{3}}{2}i=$

$=\frac{3}{2}+\frac{3}{2}=3$

$zz^{*}=(\frac{3}{2}-\frac{\sqrt{3}}{2}i)(\frac{3}{2}+\frac{\sqrt{3}}{2}i)=$

$=[\frac{3}{2}]^{2}-[\frac{\sqrt{3}}{2}]^{2}*i^{2}=\frac{9}{4}+\frac{3}{4}=3$

$\frac{z}{z^{*}}=\frac{(\frac{3}{2}-\frac{\sqrt{3}}{2}i)}{(\frac{3}{2}+\frac{\sqrt{3}}{2}i)}=\frac{3-\sqrt{3}i}{3+\sqrt{3}i}=\frac{(3-\sqrt{3}i)^{2}}{(3+\sqrt{3}i)(3-\sqrt{3}i)}=\frac{9-6\sqrt{3}i+3i^{2}}{9-3i^{2}}=\frac{6-6\sqrt{3}i}{12}=$

$=\frac{6}{12}-\frac{6\sqrt{3}}{12}i=\frac{1}{2}-\frac{\sqrt{3}}{2}i$

б) Запишем наше комплексное число в тригонометрической форме:

$z=r(cos\phi+isin\phi)$ --------(1)

где модуль комплексного числа

В нашем случае

$r=\sqrt{(\frac{3}{2})^{2}+(\frac{\sqrt{3}}{2})^{2}}=\sqrt{\frac{9}{4}+\frac{3}{4}}=\sqrt{3}$ ---------(2)

Итак, число в тригонометрической форме с учетом (1) и (2):

$z=\sqrt{3}(cos\phi+i*sin\phi)$

Для нахождения четвертой степени числа применим формулу Муавра при n=4 :

$z^{4}=(\sqrt{3})^{4}(cos4\phi+i*sin4\phi)=9(cos4\phi+i*sin4\phi)($

Известно, что корень n-й степени из комплексного значения имеет n различных значений. В нашем случае нужно найти корень 2-й степени, а значит корень 2-й принимает два различных значения.

$\sqrt{z^{4}}=\sqrt{9}(cos\frac{4\phi+2k\pi}{2}+i*sin\frac{4\phi+2k\pi}{2})$