ответ: x²*y²+x²/y²=C.
Пошаговое объяснение:
Запишем равнение в виде P*dx+Q*dy=0, где P=x*y²+x/y² и Q=x²*y-x²/y³. Найдём частные производные dP/dy и dQ/dx: dP/dy=2*x*y-2*x/y³, dQ/dx=2*x*y-2*x/y³. Так как dP/dy=dQ/dx, то левая часть данного уравнения представляет собой полный дифференциал du некоторой функции u(x,y). Отсюда P=du/dx=x*y²+x/y² и тогда u=∫(x*y²+x/y²)*dx=1/2*x²*y²+1/2*x²/y²+f(y), где f(y) - неизвестная пока функция от y. Дифференцируя это выражение по y и приравнивая к Q, приходим к уравнению x²*y-x²/y³+f'(y)=x²*y-x²/y³. Отсюда f'(y)=0 и тогда f(y)=C1, где C1 - произвольная постоянная. И так как du=0, то u=const и поэтому u(x,y)=1/2*x²*y²+1/2*x²/y²+C1=C2, где C2 - также произвольная постоянная. Отсюда, полагая C2-C1=C3, получаем 1/2*x²*y²+1/2*x²/y²=С3, или, полагая 2*С3=С, x²*y²+x²/y²=C.
(0; 1)∪{3}
Пошаговое объяснение:
Перенесём в левую часть x и рассмотрим функцию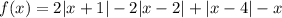 
. Нули модулей: x = -1, x = 2, x = 4. Рассмотрим функцию относительно этих чисел:
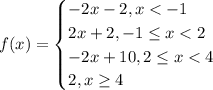
Эту функцию получили так: в первом случае все модули превратили в скобки и перед ними поставили знак минус, упростили. Во втором — то же самое, но перед первым модулем ставим знак плюс. И так далее.
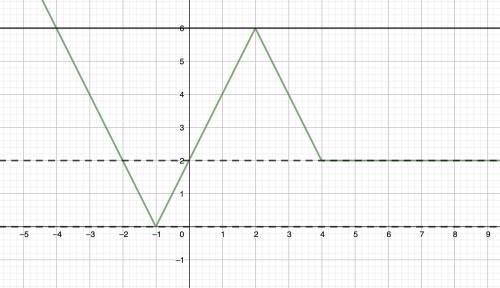
Построим график данной функции — строим прямые при указанных ограничениях (на рисунке отмечен зелёным). Посчитаем значения функции в точках "сгиба": f(-1) = 2·(-1)+2 = 0, f(2) = -2·2+10 = 6, f(4) = 2.
y = 2a — прямая, параллельная оси Ox. Если 2a < 0, то уравнение не имеет корней (нет пересечений), если 2a = 0, уравнение имеет один корень, если 0 < 2a < 2, уравнение имеет два корня, если 2a = 2, уравнение имеет бесконечно много корней, если 2 < 2a < 6, уравнение имеет три корня, если 2a = 6, уравнение имеет два корня, если 2a > 6, уравнение имеет один корень.
Подходящие значения параметра a: 0 < 2a < 2 ⇔ 0 < a < 1; 2a = 6 ⇔ a = 3.
Лвтталвдвь 6626262