a) Р = ( а + b ) × 2
P = ( 15 + 25 ) × 2 = 80 cm
Oтвет: 80 cm
b) a = ( P - 2b ) ÷ 2
a = ( 122 - 2 × 34 ) ÷ 2 = 27 m
ответ: 27 m
. 
.
.
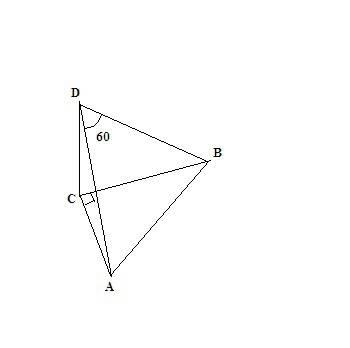
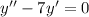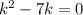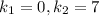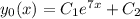, где C1, C2 - произвольные постоянные.
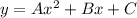следует умножить на x и в таком виде искать решение. То есть, ищем частное решение неоднородного уравнения в виде 
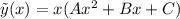, где A, B, C - неизвестные числа.
.
.
.
.
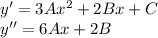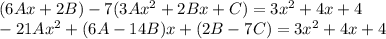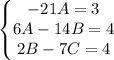
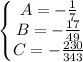
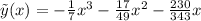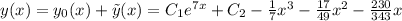a)Р=2×(а+b)=2×(15×25)=2×40=80см
б)а+b=P/2
а=Р/2-b=122/2-34=61-27=34м