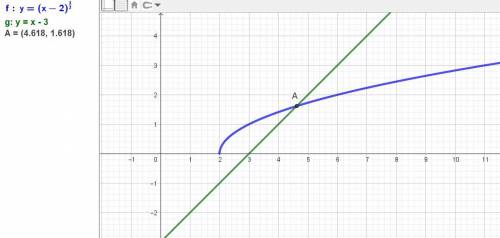
Дано уравнение: √(x - 2) = x - 3.
ОДЗ: х - 2 > 0, x > 2.
Надо обе части уравнения возвести в квадрат.
х - 2 = х² - 6х + 9.
Получаем квадратное уравнение:
х² - 7x + 11 = 0.
Квадратное уравнение, решаем относительно x:
Ищем дискриминант:
D=(-7)^2-4*1*11=49-4*11=49-44=5;
Дискриминант больше 0, уравнение имеет 2 корня:
x_1=(√5-(-7))/(2*1)=(√5+7)/2=√5/2+7/2=√5/2+3.5~~4.618034;
x_2=(-√5-(-7))/(2*1)=(-√5+7)/2=-√5/2+7/2=-√5/2+3.5~~2.381966.
Получили 2 корня - это результат лишнего корня при возведении в квадрат, но должна быть одна точка пересечения одной ветви параболы и прямой.
Второй корень не подходит.
ответ: х1 = √5/2+3,5.
3/8
Пошаговое объяснение:
Сначала действие в скобках:
2/15+7/12=8/60+35/60=43/60
Теперь умножение:
(43/60)х(30/43)=30/60=1/2
Теперь деление:
2/(5/2)=4/5
Теперь второе умножение:
(4/5)х(5/32)=4/32=1/8
Теперь вычитание:
1/2-1/8=3/8