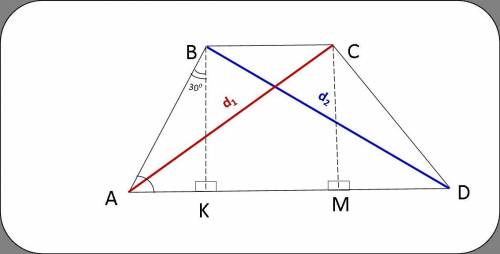
1) Опустим перпендикуляры из вершин В и С.
ВК⊥AD и CM⊥AD
2) Рассмотрим ΔАВК.
∠ВАК = 60° по условию;
∠АКВ = 90° по построению;
∠АВК = 180° - (90°+60°) = 30°
2) Катет АК против угла 30°, потому он равен половине гипотенузы АВ.
АК = 10 см : 2 = 5см
3) По построению ВК⊥AD и CM⊥AD, значит,
KBCM - прямоугольник ==> BC = KM = 6 см
ВК = СМ
4) АМ = АК + КМ
АМ = 5см + 6см = 11см
5) МD = АD - АК
МD = 16см - 11см = 5см
6) Если AK = MD = 5см,
∠AKB = ∠BMD = 90°
ВК = СМ
значит, ΔАВК = ΔCDM => AB = CD => ABCD - равнобочная трапеция => значит её диагонали равны между собой.
7) ΔАВК -прямоугольный, значит, можно применить теорему Пифагора.
АК² + ВК² = АВ²
ВК² = 10² - 5²
ВК = 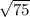
ВК = СМ = 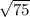
7) ΔАСМ -прямоугольный. По теореме Пифагора найдем АС.
АС² = АМ² + СМ²
АС² = 11² + (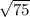 )²
)²
АС = 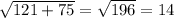 см
см
АС = 14 см
8) AC = BD = 14см
ответ: 14см; 14см
запишите суммы в десятичной системе счисления
3*1000+2*100+4*10+5= 3245.
1)) 3•1000=3000
2)) 2•100=200
3)) 4•10=40
4)) 3000+ 200+ 40+ 5= 3245
запишите суммы с римских цифр
III • M+ II • C+ IV • X= MMMCCXLV.
1)) III•M=MMM
2)) II•C=CC
3))IV•X=XL
4)) MMM+ CC+XL+V=MMMCCXLV
1=I;
5=V;
10=X
50=L
100=C
500=D
1000=M
Пошаговое объяснение:
Числа записываем так; если меньшее число впереди (слева) до пяти и в десятках до 50, в сотнях до 500; все надо вычитать; если после них (справа), то прибавлять.
например
14, это 10+ 5-1; пишем 10, X, вперёд неё пишем 5, V и ещё вперёд 1, I; получили IVX; или 9, это 10-1; пишем Х, вперёд 1, I, 9= IX;
(x-4 8/5)×3/7=7 5/10
x-28/5=75/10÷3/7=75/10×7/3=25/10×7/1
x-28/5=175/10=35/2
x=175/10+28/5=175/10+56/10
x=231/10=23 1/10=23,1
(231/10-56/10)×3/7=75/10
175/10×3/7=75/10
25/10×3/1=75/10
75/10=75/10
7 5/10=7 5/10