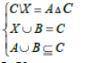
Пусть этот отрезок равен 12 см(так как 12 пунктиров, так же для того чтобы решить эту задачу нужен рисунок) -
1)в 1/3 части будет 4 см -
|||| (т.к мы разделили этот отрезок на 3 части и в одной части - 4 пунктира(т.е. см))
в 1/6 части будет 2 см -
|--|--|--|--|--|--| (т.к. мы разделили этот отрезок на 6 частей и в одной части - 2 пунктира)
в 1/12 части будет 1 см -
|-|-|-|-|-|-|-|-|-|-|-|- | (т.к. мы разделили этот отрезок на 12 частей и в одной части - 1 пунктир)
2) в 2/3 части будет 8 см -
|||| (т.к мы разделили этот отрезок на 3 части и в двух частях - 8 пунктиров (т.е. см))
в 5/6 части будет 10 см -
|--|--|--|--|--|--| (т.к. мы разделили этот отрезок на 6 частей и в пяти частях - 10 пунктиров)
в 11/12 части будет 11 см -
|-|-|-|-|-|-|-|-|-|-|-|-| (т.к. мы разделили этот отрезок на 12 частей и в одиннадцати частях - 11 пунктиров)
Відповідь:
Покрокове пояснення:
Из уравнения А∪В⊆С следует, что и А и В есть подмножество С
Из Х∪В=С, что Х также есть подмножеством С и вместе с В даёт С, тесть Х есть дополнением В к С или Х⊆В, тогда В=С или Х и В пересекаются и полностью покрывают С . Тогда или А⊆Х , или они пересекаются, или нет
Учитывая 3 А ⊆С в правой части 1 уровня имеем АΔС=А\С∪С\А=С\А, поэтому С\Х=С\А, это может быть когда Х=А
Система совместима, когда Х=А⊆С
Несовместимы, когда Х и А не равны, не пересекаются