
Чтобы найти НОК нескольких чисел, надо разложить эти числа на простые множители и найти произведение всех простых множителей, взятых с наибольшим показателем степени.
а) 21 = 3 · 7 28 = 2² · 7
НОК (21 и 28) = 2² · 3 · 7 = 84 - наименьшее общее кратное
84 : 21 = 4; 84 : 28 = 3
- - - - - - - - - - - -
б) 18 = 2 · 3² 72 = 2³ · 3²
НОК (18 и 72) = 2³ · 3² = 72 - наименьшее общее кратное
72 : 18 = 4; 72 : 72 = 1
- - - - - - - - - - - -
в) 3 и 5 - простые числа; 25 = 5²
НОК (3; 5 и 25) = 3 · 5² = 75 - наименьшее общее кратное
75 : 3 = 25; 75 : 5 = 15; 75 : 25 = 3
задача имеет решение, если в ней написано хотя бы 350 МЕТРОВ! (хотя более реальная скорость была бы при 35м)
Когда первый пол часа, то есть t₁=30 мин, второй уже круг 9 минут назад.
То есть 2-й круг за t₂=30-9=21 мин или 21/60=7/20=0.35 часа
Пусть скорость первого бегуна v₁=x км/ч, тогда 2-го: v₂=x+4 км/ч
Если второй бегун круг со скоростью v₂ за время t₂, то его путь (длина окружности) составляет: S=v₂t₂=(x+4)*0.35.
Первому бегуну до конца круга оставалось 350 м=0,35 км, значит за пол часа он путь: S₁=S-0.35=(x+4)*0.35 -0.35 км
и это расстояние он за 1/2 часа, тогда его скорость будет равна:
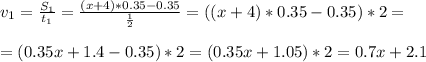
с другой стороны мы обозначили скорость 1-го бегуна за х, значит:
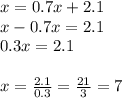
ответ: 7 км/ч
1)114; 2)95; 3)59
Пошаговое объяснение: