
Имеем 3 интервала, на каждом из которых функция задана непрерывными выражениями. Значит нужно проверить 2 точки-границы соседних интервалов
\begin{gathered}1) $ $ x=0 \lim_{x \to 0-0}\, (x-1)=-1 \lim_{x \to 0+0} \. (x^2)=0\end{gathered}
Предел слева не равен пределу справа, оба предела конечные. Значит это неустранимая точка разрыва первого рода
\begin{gathered}2) $ $ x=2 \lim_{x \to 2-0} \, (x^2)=4 \lim_{x \to 2+0}\, (2x)=4\end{gathered}
Предел слева равен пределу справа, оба предела конечные. Значит это устранимая точка разрыва первого рода
На всякий случай прикреплю график функции f(x)
Встреча Иванова и Ивановского произошла ближе к городу А.
Пошаговое объяснение:
Вспомним:
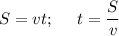
Пусть х км/ч - скорость Петрова, тогда 2х - скорость Иванова;
пусть у км/ч - скорость Петровский, тогда 3у - скорость Ивановского.
Расстояние примем за S.
1. Рассмотрим Иванова и Петровского.
Скорость сближения:
(2х+у) км/ч
⇒ Время до встречи:
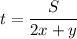 (ч)
(ч)
2. Рассмотрим Петрова и Ивановского:
Скорость сближения:
(х+3у) км/ч
⇒ Время до встречи:
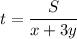 (ч)
(ч)
Так как они выехали одновременно и встретились одновременно, то их время до встречи равно:
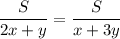
или
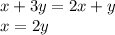
То есть:
Скорости Петрова - 2у км/ч, Иванова - 4у км/ч.
3. Рассмотрим Иванова и Ивановского.
Скорость их сближения:
4у + 3у = 7у (км/ч)
Время до встречи:
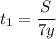 (ч)
(ч)
⇒ Иванов отъехал от А:
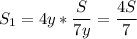 (км)
(км)
4.рассмотрим Петрова и Петровского:
Скорость сближения:
2у+у=3у (км/ч)
Время до встречи:
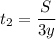 (ч)
(ч)
⇒ Петров отъехал от А:
 (км)
(км)
Сравним S₁ и S₂:
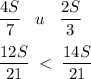
Встреча Иванова и Ивановского произошла ближе к городу А.
*В задаче скорость велосипедиста больше скорости мотоциклиста! )))

12 км
Пошаговое объяснение:
предполагается видимо, что они выехали в одну сторону, а не на встречу друг другу.
один велосипедист догоняет другого, так как движется быстрее, скорость сближения = разность скоростей велосипедистов = 17 - 15 км/ч
= 2 км/ч, значит через 2 часа они станут на 2 · 2 = 4 км ближе друг к другу чем в момент старта. А в момент старта они находились на расстоянии 16 км, значит через 2 часа они будут на расстоянии 16 - 4 = 12 км