ответ
Дано:
Дано:Пешеход преодолел путь в 2 километра.
Дано:Пешеход преодолел путь в 2 километра.2 километра - это 2/11 всего расстояния между пунктами А и В.
Дано:Пешеход преодолел путь в 2 километра.2 километра - это 2/11 всего расстояния между пунктами А и В.Пешеход только 2 части из 11, найдем, сколько километров составляют только одну часть пути:
Дано:Пешеход преодолел путь в 2 километра.2 километра - это 2/11 всего расстояния между пунктами А и В.Пешеход только 2 части из 11, найдем, сколько километров составляют только одну часть пути:2 : 2 = 1 километр.
Дано:Пешеход преодолел путь в 2 километра.2 километра - это 2/11 всего расстояния между пунктами А и В.Пешеход только 2 части из 11, найдем, сколько километров составляют только одну часть пути:2 : 2 = 1 километр.Вычислим расстояние между пунктами А и В, то есть сколько километров составляют все 11 частей:
Дано:Пешеход преодолел путь в 2 километра.2 километра - это 2/11 всего расстояния между пунктами А и В.Пешеход только 2 части из 11, найдем, сколько километров составляют только одну часть пути:2 : 2 = 1 километр.Вычислим расстояние между пунктами А и В, то есть сколько километров составляют все 11 частей:11 * 1 = 11 километров.
Дано:Пешеход преодолел путь в 2 километра.2 километра - это 2/11 всего расстояния между пунктами А и В.Пешеход только 2 части из 11, найдем, сколько километров составляют только одну часть пути:2 : 2 = 1 километр.Вычислим расстояние между пунктами А и В, то есть сколько километров составляют все 11 частей:11 * 1 = 11 километров.ответ: от пункта А до пункта В 11 километров.
Можно сердечко? ;з
(см. объяснение)
Пошаговое объяснение:
Вынесении общего множителя за скобки.
Рассмотрим пример:
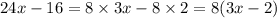
Хорошо видно, что и 24 и 16 делятся на 8. Тогда 8 - это общий множитель, который можно вынести за скобки. Далее делим исходное выражение на 8 и отправляем полученное в скобки.
Попробуйте решить самостоятельно:
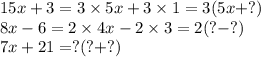
(ответы в конце объяснения)
Вынесении многочлена за скобки:
Прием тут аналогичен описанному выше.
Рассмотрим пример:
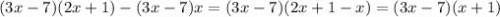
Здесь все то же самое, только за скобки выносится общая часть.
При этом не нужно бояться выражения в скобках!
Если оно одинаково, то смело пользуйтесь приемом:
![(\sqrt[7]{x}+\arcsin (x))(\cos(x)+\sqrt[7]{x})-(\sqrt[7]{x}+\arcsin (x))^2=\\=(\sqrt[7]{x}+\arcsin (x))(\cos(x)+\sqrt[7]{x}-(\sqrt[7]{x}+\arcsin (x)))=\\=(\sqrt[7]{x}+\arcsin (x))(\cos(x)-\arcsin (x))](/tpl/images/1643/8776/95ae2.png)
Каким бы страшным не показалось семикласснику это выражение, прием остается 100% таким же!
Группировка.
Рассмотрим пример:
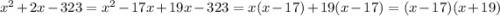
Здесь необходимо представить 2x, как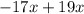 
. После чего воспользоваться знаниями выше.
Иногда сразу дают выражение вида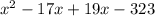 
, что упрощает ситуацию.
ответы к заданиям для самостоятельного решения.
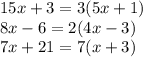
Объяснение завершено!
х1=0,5
х2=2
(-бесконечности;0,5)
ответ:-1,5,0,