Если посмотреть на число 31, то можно понять, что оно очень близко к числу 32, что есть пятой степенью двойки. И при этом 1г гири +31 г сахара =32г
Попробуем разложить 32 на сумму степеней двойки
2^1=2
2^2=4
2^3=8
2^4=16
2^5=32, но
2+2+4+8+16=32
Мы не можем первым разом получить 2г сахара, а только 1, поэтому из 2-х грамм 1г гиря.
То есть за первый раз мы отмеряем 1г сахара с гири (общая масса 2г,как первая степень двойки)
Потом за вторым с гири и 1г сахара отмеряем 2г (общая масса 4г,квадрат)
За третьим 1г гири, 1г и 2г отмеряем 4г сахара (общая масса 8г,куб)
За четвертым все то, что измеряли дает повод отмерять 8г сахара(четвертая степень)
И за последним мы отмеряем 16г сахара.
Итого 1+2+4+8+16=31.
2) исходное выражение = sin( 4*(п/4) - 2*(п/3) ) = sin(п - (2/3)*п) =
= sin(п/3) = (V3)/2.
3) x = arccos(-0,3328) + 2*п*n, или x=-arccos(-0,3328) + 2*п*n, n - принимает все целые значения.
x = (п - arccos(0,3328) ) + 2*п*n, или
x = -(п-arccos(0,3328) ) + 2*п*n = arccos(0,3328) - п + 2*п*n.
4) 1 - 2*sin^2(x/2) = cos(x),
sin^2(x/2) = (1-cos(x))/2.
(1-cos(x))/2 = 3/4.
1- cos(x) = 3/2.
cos(x) = 1 - (3/2) = -1/2.
x = arccos(-1/2) + 2*п*n, или
x = -arccos(-1/2) + 2*п*n, n принимает все целые значения,
arccos(-1/2) = п - arccos(1/2) = п - (п/3) = (2/3)*п,
x = (2/3)*п + 2*п*n, или
x = -(2/3)*п + 2*п*n.
5) tg(3x+30) = (V3).
3x+30 = 60 + 180*n,
3x = 30 + 180*n,
x = 10 + 60*n.
(x выражено в градусах, n - пробегает все целые значения).
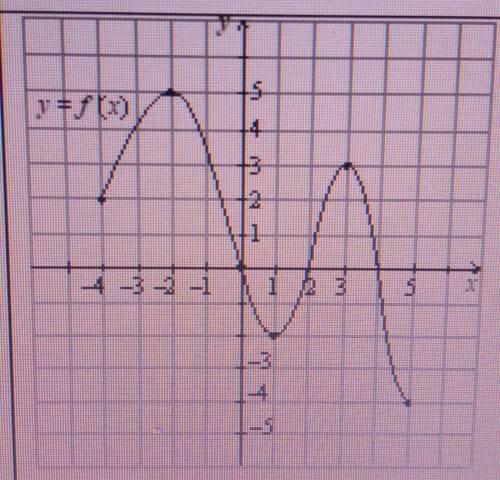
6) см. прикрепленный рисунок.