Можно Лучший?
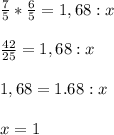
Большая сторона первоначального прямоугольника x.
Есть два возможный варианта: 1) прямоугольник разрезали по меньшей стороне; 2) прямоугольник разрезали по большей стороне. Рассмотрим их оба:
1) пусть одна сторона первого прямоугольника y, тогда вторая 6-y. Вторые стороны у обоих x.
Площади: xy кв.ед. у первого, x·(6-y) кв.ед. у второго. У первого в 3 раза больше:
xy = 3x·(6-y)
Периметры: (x+y)·2 у первого, (x+6-y)·2 у второго. У первого в 2 раза больше:
(x+y)·2 = 2·(x+6-y)·2
Составим и решим систему уравнений:

Большая сторона первоначального прямоугольника 1,5.
2) пусть одна сторона первого прямоугольника y, тогда вторая x-y. Вторые стороны у обоих 6.
Площади: 6y кв.ед. у первого, 6(x-y) кв.ед. у второго. У первого в 3 раза больше:
6y = 3·6(x-y)
Периметры: у первого (y+6)·2, у второго (x-y+6)·2, у первого в 2 раза больше:
(y+6)·2 = 2·(x-y+6)·2.
Составим и решим систему уравнений:
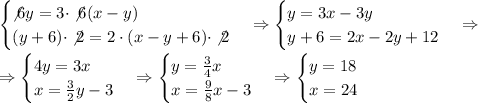
Большая сторона первоначального прямоугольника 24.
ответ: 1,5 или 24.
25
Пошаговое объяснение:
x - скорость лайнера, км/ч.
y - скорость сухогруза, км/ч.
z - скорость течения, км/ч.
1 ч 36 мин = 1 ч + 36/60 ч = 1 ч + 3/5 ч = 8/5 ч
1) Если лайнер и сухогруз идут в одном направлении по течению реки.
Система уравнений:
100/((x+z)-(y+z))=8 |4
100/((x+z)+(y-z))=8/5 |4
25=2(x+z-y-z); x-y=25/2
25·5=2(x+z+y-z); x+y=125/2
x+y-x+y=125/2 -25/2
2y=100/2
y=50/2=25 км/ч - скорость сухогруза.
2) Если лайнер и сухогруз идут в одном направлении против течения реки.
Система уравнений:
100/((x-z)-(y-z))=8 |4
100/((x-z)+(y+z))=8/5 |4
25=2(x-z-y+z); x-y=25/2
25·5=2(x-z+y+z); x+y=125/2
Решение смотри выше.
y=25 км/ч - скорость сухогруза.
7/5 × 6/5=1.68:x
42/25=1.68:x
1.68=1.68:x
x=1