20 см
Пошаговое объяснение:
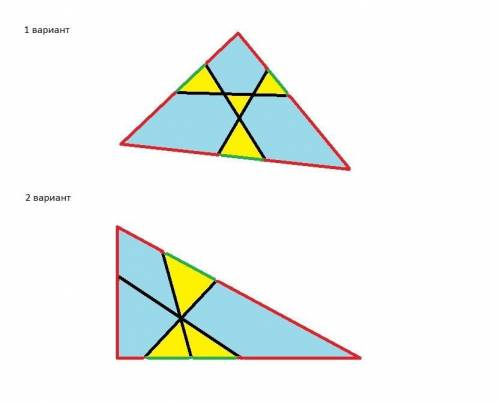
Возможно в условии ошибка: разделить тремя отрезками треугольник, чтобы получить 4 треугольника и 3 прямоугольника не получается. Так разделить можно четырехугольник. Треугольник можно разделить тремя отрезками на 3 треугольника и 3 пятиугольника (см.рисунок Вариант 1). Если разделить треугольник на 3 треугольника и 3 четырехугольника (см.рисунок Вариант 2), такой вариант не подходит, т.к. для решения надо, чтобы треугольники не имели смежных сторон, т.е. не соприкасались друг с другом, а были разделены многоугольниками - пятиугольниками см. рисунок 1 вариант.
В таком (см.рисунок вариант 1) и подобных случаях алгоритм решения задачи будет одинаковый:
так, как отрезки являются всеми внутренними сторонами и внутренних треугольников и внутренних четырехугольников или других многоугольников, то если мы отнимем от суммы периметров треугольников длину отрезков, т.е. длину их всех сторон, находящихся внутри треугольника (на рисунке черным цветом), то получим длину всех внешних сторон треугольников (4-угольников, 5-угольников и т.д.), т.е. длину их сторон, которые лежат на сторонах исходного большого треугольника (на рисунке внешние стороны показаны зеленым цветом, а внешние стороны 4х и 5-угольников - красным). Как видно на риисунке, сумма внешних сторон треугольников и 4-угольников (5-угольников) равна периметру исходного большого треугольника (красные стороны плюс зеленые), отсюда:
(Pм.тр. - Pотр.) + (Pчет. - Pотр.) = Pб.тр.
Pм.тр. + Pчет. - 2*Pотр. = Pб.тр.
19 + 35 - 2*17 = Pб.тр. ;
Pб.тр. = 20 см.
Молча...)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
А(-1;0),В(4;0),С(1;-2), найти:
1) уравнение высоты АД.
Высота АД – это перпендикуляр к стороне ВС.
Вектор ВС = (1-4; -2-0) = (-3; -2).
Уравнение прямой ВС: (х – 4)/(-3) = у/(-2) каноническое
-2х + 8 = -3у
2х - 3у – 8 = 0 общее.
Для прямой в общем виде Ax + By + C = 0 перпендикулярная прямая меняет коэффициенты А и В на –В и А (из условия, что их скалярное произведение равно 0).
Тогда уравнение перпендикулярной прямой к прямой ВС будет иметь вид:
3x + 2y + С = 0. Для определения слагаемого С подставим координаты точки А(-1; 0).
3*(-1) + 2*0 + C = 0, отсюда С = 3.
ответ: 3x + 2y + 3 = 0.
2) уравнение прямой, проходящей через А параллельно ВС.
Коэффициенты при переменных у этой прямой такие же, как и у прямой ВС: 2х - 3у + С = 0. Подставим координаты точки А(-1; 0).
2*(-1) – 3*0 + С = 0, отсюда С = 2.
Получаем уравнение 2х - 3у + 2 = 0.
3) уравнение прямой, соединяющей середины сторон АВ и ВС.
Коэффициенты при переменных у этой прямой такие же, как и у прямой АС. Вектор АС = С(1;-2) - А(-1;0) = (2; -2).
Уравнение АС: (х + 1)/2 = у/(-2) или х + у + 1 = 0.
Найдём середину Д стороны АВ.
Д = (А(-1;0)+В(4;0))/2 = (1,5; 0).
Подставим координаты точки Д в уравнение прямой х + у + С = 0.
1,5 + 0 + С = 0, отсюда С = -1,5.
Уравнение х + у - 1,5 = 0 или в целых числах 2х + 2у - 3 = 0.
4) угол А треугольника АВС. А(-1;0),В(4;0),С(1;-2).
Находим векторы и их модули.
АВ = (4-(-1); 0-0) = (5; 0). |AB| = 5.
AC = (2; -2). |AC) = √(2² + (-2)²) = √(4 + 4) = √8 = 2√2.
Теперь находим косинус угла А.
cos A = (5*2 + 0*(-2))/(5*2√2) = 10/(10√2) = 1/√2.
Угол А = arccos(1/√2) = 45 градусов.