Відповідь:
Покрокове пояснення:
Вероятность забить гол- p=0.7
Вероятность не попасть в ворота- q=0.3
К- количество забитых мячей
Р(к=4)=С(4,6)р⁴q²=6!/4!2! ×0.7⁴×0.3²=0,324135
Р(к<=4)=Р(к=0)+Р(к=1)+Р(к=2)+Р(к=3)+Р(к=4)=q⁶+6pq⁵+15p²q⁴+20p³q³+15p⁴q²=
0.000729+0,010206+0.059535+0.18522+0.324135=0,579825
Р(к<=4)=1-Р(к>4)=1-(Р(к=5)+Р(к=6)=1-(6p⁵q+p⁶)=1-0,420175 =0,579825
Вася выкинул 2 карточки с числами 3 и 6. Оставшиеся поделил на 28+8 и 20+12+4
Пошаговое объяснение:
Чтобы оставшаяся сумма могла поровну поделиться на 2 надо выкинуть карточку с нечетным числом. У нас это единственная карточка с числом 3. Тогда сумма 81-3=78, 78:2=39, но у нас не получится из оставшихся каточек собрать сумму в 39, значит не получится выкинуть только одну карточку. Попробуем выкинуть две карточки, но чтобы в сумме они давали нечетное число, допустим карты 3 и 4, тогда 81-7=74, 74/2=37.Но оставшиеся карточки не дадут в сумме 37. Значит выбрали не ту карту, надо оставить карту 4 и убрать вместо нее 6. Итак, убираем 3+6=9. 81-9=72, 72/2=36 Попробуем распределить карты на две стопки, чтоб каждая кучку в сумме давала 36. Это будут 28 +8 = 20+12+4. Получилось. В одной куче 28 и 8, в другой 20, 12 и 4. Пришлось выкинуть две карты 3 и 6.
Задача на формулу Бернулли: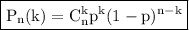
Вероятность успеха в одном испытании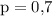 , тогда
, тогда 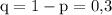 .
.
Всего испытаний проведено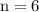 .
.
1) Вероятность того, что футболист забьёт пенальти ровно четыре раза:
2) Вероятность того, что футболист забьёт пенальти не более четыре раза: