Question

Найдите область определения функции:(примеры прикреплены ниже)

Answer 1

1 (-бесконечность;+бесконечность) 2 (- бесконечность;-7\4)U(-7\4;+бесконечность) 3 [-7;+бесконечность) 4 (-бесконечность;1/2) 5(-бесконечность;3)U(-3;0)U(0;3)U(3;+бесконечность) 6(-бесконечность;+бесконечность)

Пошаговое объяснение:

Область определения это такие числа, которые может принимать переменная x.

1.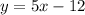 $y=5x-12$ (здесь при любых числах выражение решается,т.е. нет ограничений => (-бесконечность;+бесконечность)

2.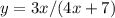 $y=3x/(4x+7)$ (В данном случае, ограничение присутствует, знаменатель дроби не должен быть равен нулю. (старое правило-на 0 делить нельзя)

$4x+7 \neq 0$

$x \neq -7/4$ => (- бесконечность;-7\4)U(-7\4;+бесконечность)

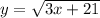3.$y=\sqrt{3x+21}$ (Под корнем всегда должно быть неотрицательное число)

$3x+21\geq 0\\x\geq -7$[-7;+бесконечность)

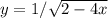4.$y=1/\sqrt{2-4x}$ (знаменатель не должен быть равен 0, а так же не должен быть отрицательным)

$2-4x0\\x$(-бесконечность;1/2)

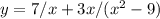5. $y=7/x+3x/(x^{2} -9)$ (знаменатель не должен быть равен 0)

$x\neq 0 и x^{2} -9\neq 0\\x\neq 0 и (x-3)(x+3)\neq 0\\x\neq 0 и x\neq +-3$(-бесконечность;3)U(-3;0)U(0;3)U(3;+бесконечность)

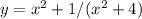6.$y=x^{2} +1/(x^{2} +4)\\\\$ (знаменатель не должен быть равен 0, но если решить, можно понять что знаменатель положителен при любых x)

(-бесконечность;+бесконечность)