Пошаговое объяснение:
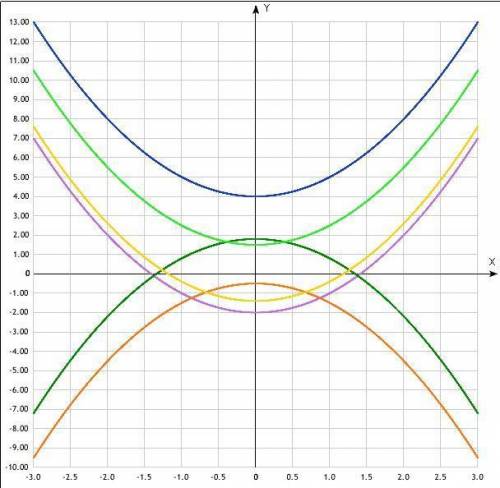
Все функции - параболы вида
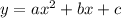
a - определяет "ширину" ветвей, при 0<а<1 ветви "шире", при а > 1 "уже"
При отрицательном а - ветви направлены вниз, при положительном вверх. В 3 и 4 примерах а = -1, поэтому ветки вниз
b - (в данных примерах не используется) показывает смещение вершины параболы вдоль оси OX, положительный левее, отрицательный правее от оси OY
с - смещение вершины графика вдоль оси OY - положительный с - выше, отрицательный ниже, при с=0 ветка графика пересекает точку 0,0
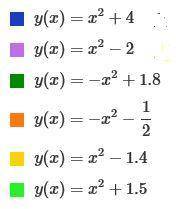
Таким образом в каждом автобусе предполагалось разместить n/х студентов.
К назначенному времени два автобуса не прибыли, то есть студентов разместили в х-2 автобусах, по n/(х-2) студентов в каждом. Получилось, что в каждый автобус пришлось посадить на 7 человек больше, чем предполагалось то есть:
n/(х-2)=n/x +7
n/(х-2)-n/x -7=0
(nx-n(x-2)-7x(x-2))/(x(x-2))=0
(nx-nx+2n-7x^2+14x)/(x(x-2))=0
(2n-7x^2+14x)/(x(x-2))=0
2n-7x^2+14x=0 x(x-2) не равно 0
D/4=7^2-(-7)*2n=49+14n x не равно 0 или x-2 не равно 0
x=(-7+-(49+14n)^0.5 )/(-7) x не равно 0 x не равно 2
x=1+-(1+2n/7)^0.5
x1=1+(1+2n/7)^0.5 x2=1-(1+2n/7)^0.5
не подходит, т.к при n>0 x2<0
Таким образом , перевозкой студентов было занято x=1+(1+2n/7)^0.5 автобусов, где n - число студентов