Данная функция является квадратичной, и ее график — это парабола.
Сперва нужно определить коэффициенты а, b и c в формуле функции.
Формула абсциссы вершины параболы:
По графику видим, что абсцисса вершины равна 4.
Значит, .
Выберем две точки с целочисленными координатами, принадлежащие параболе.
Возьмем вершину, т. А (4; 1) и т. В (2; -3).
Подставим координаты точек в формулу функции: абсциссу вместо х, а ординату вместо у.
Получаем два уравнения:
1)
2)
Составим систему уравнений:
Из первого уравнения выразим коэффициент b.
Сперва умножим обе части уравнения на знаменатель дроби:
Теперь умножим обе части на -1:
Из второго уравнения вычтем третье, чтобы избавиться от коэффициента c. Отдельно вычитаем левые, отдельно правые части:
Раскроем скобки:
Приведем подобные слагаемые:
Разделим обе части уравнения на 2 для удобства:
Подставим значение коэффициента b:
Теперь найдем коэффициент b, подставив найденное значение коэффициента а в уравнение :
Подставим значения коэффициентов а и b в третье уравнение системы, чтобы найти коэффициент с:
Подставим найденные коэффициенты в формулу функции:
у = -х² + 8х - 15
Чтобы найти у(-19), подставим число -19 вместо аргумента:
ответ: -528.
Данная функция является квадратичной, и ее график — это парабола.
Сперва нужно определить коэффициенты а, b и c в формуле функции.
Формула абсциссы вершины параболы:
По графику видим, что абсцисса вершины равна 4.
Значит,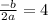 .
.
Выберем две точки с целочисленными координатами, принадлежащие параболе.
Возьмем вершину, т. А (4; 1) и т. В (2; -3).
Подставим координаты точек в формулу функции: абсциссу вместо х, а ординату вместо у.
Получаем два уравнения:
1)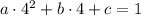
2)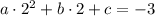
Составим систему уравнений:
Из первого уравнения выразим коэффициент b.
Сперва умножим обе части уравнения на знаменатель дроби:
Теперь умножим обе части на -1:
Из второго уравнения вычтем третье, чтобы избавиться от коэффициента c. Отдельно вычитаем левые, отдельно правые части:
Раскроем скобки:
Приведем подобные слагаемые:
Разделим обе части уравнения на 2 для удобства:
Подставим значение коэффициента b:
Теперь найдем коэффициент b, подставив найденное значение коэффициента а в уравнение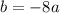 :
:
Подставим значения коэффициентов а и b в третье уравнение системы, чтобы найти коэффициент с:
Подставим найденные коэффициенты в формулу функции:
у = -х² + 8х - 15
Чтобы найти у(-19), подставим число -19 вместо аргумента:
ответ: -528.